Divergence (analyse vectorielle) - Définition

Propriétés

a)

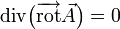
Cette formule est particulière à la dimension 3. Elle signifie qu'un champ rotationnel est à divergence nulle. Inversement, si un champ de vecteurs sur un ouvert étoilé de est à divergence nulle, il existe un champ tel que

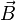
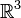
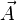
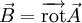
(on dit alors que est un potentiel vecteur). Cette propriété, une fois convenablement interprétée en termes de formes différentielles, est une application directe du lemme de Poincaré).

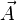
Attention. Le champ newtonien est à divergence nulle, mais il n'existe pas de champ de vecteurs tel que . En effet, si tel était le cas, son flux à travers toute surface fermée serait nul, alors que son flux à travers les sphères centrées à l'origine vaut 4π. En fait, ce champ n'est défini que sur l'espace privé de l'origine, qui n'est pas un ouvert étoilé : le lemme de Poincaré ne s'applique pas.

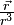
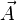
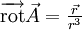
b)

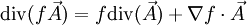
D'après le théorème de Stokes, l'intégrale sur de la divergence d'un champ de vecteurs nul en dehors d'une partie bornée est nulle. Par conséquent, si f est une fonction lisse et un champ de vecteurs, tous deux nuls en dehors d'une partie bornée (cette condition assurant que les intégrales ont un sens),

.

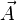
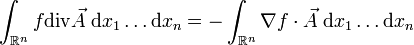
Cette propriété s'interprète de la façon suivante. Soient et respectivement les espaces vectoriels des fonctions lisses et des champs de vecteurs sur . On les munit des produits scalaires

et

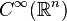
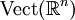
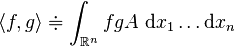
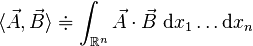
Alors , ce qui permet de voir l'opérateur divergence comme le transposé (au signe près) de l'opérateur gradient.

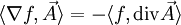
Cette interprétation de la divergence présente l'avantage de se généraliser aussi bien aux variétés riemanniennes qu'aux tenseurs.

c)

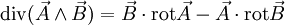
Une application typique de cette formule est le théorème de Poynting en électromagnétisme.

d)

Ces relations, très utilisées en analyse vectorielle, se comprennent mieux dans le cadre des formes différentielles.

Divergence d'un tenseur

Cas des espaces euclidiens

Un tenseur de type (p,q) (p-contravariant et q- covariant) est donné par ses coordonnées . Sa dérivée covariante est alors par définition le tenseur de type (p,q + 1) donné par (on a désigné par l'opérateur de dérivation par rapport à la i-ième variable). La divergence est le tenseur de type (p − 1,q) défini par

Exemple  :

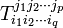
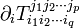
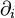
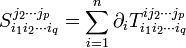
La divergence du tenseur

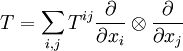
(qui est de type (2,0)) est le champ de vecteurs

avec

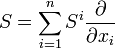
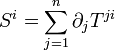
Cas général

Cette définition s'étend pratiquement mot pour mot aux tenseurs sur une variété munie d'une connexion. Dans les formules précédentes, on remplace la différentiation par l'opérateur de différentiation covariante , qui à partir d'un tenseur de type (p,q) donne un tenseur de type (p,q + 1), puis on pose

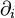
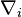
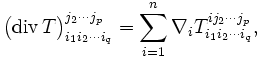
ce qui donne un tenseur de type (p − 1,q)

Le cas le plus important est celui des variétés riemanniennes ou pseudo-riemanniennes, munies de leur connexion de Levi-Civita. La métrique permet d'identifier entre eux les tenseurs de même ordre total p + q. La divergence d'un tenseur d'ordre k sera un tenseur d'ordre k − 1.

Les cas les plus utilisés (avec celui des champs de vecteurs vu plus haut) sont ceux des tenseurs symétriques d'ordre 2 et des formes différentielles.