Divergence (analyse vectorielle) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Articles d'analyse vectorielle | |

| |
| Objets d'étude | |
| Champ vectoriel | Champ scalaire |
| Équation aux dérivées partielles | |
| de Laplace | de Poisson |
| Opérateurs | |
| Nabla | Gradient |
| Rotationnel | Divergence |
| Laplacien scalaire | Bilaplacien |
| Laplacien vectoriel | D'alembertien |
| Théorèmes | |
| de Green | de Stokes |
| de Helmholtz | de flux-divergence |
| du gradient | du rotationnel |
En géométrie, la divergence d'un champ de vecteurs X mesure le défaut à ce que son flot préserve une forme volume Ω. La divergence de X, notée div X, est une fonction à valeurs réelles qui mesure la variation première de Ω le long des trajectoires du champ X. Des définitions plus précises sont données dans le corpus de l'article. L'opérateur divergence est un opérateur différentiel linéaire aux dérivées partielles premières, qui envoie un champ tensoriel d'ordre k en un champ d'ordre k − 1.
En raison de son utilisation dans les calculs de flux de champ de vecteurs, il intervient en physique pour exprimer des lois de conservation ainsi que pour la formulation locale des lois physiques faisant intervenir un champ suivant une loi en carré inverse de la distance. L'opérateur divergence est notamment utilisé dans les équations de la mécanique des fluides ou les équations de Maxwell.
Divergence d'un champ de vecteurs
Définition en dimension 3
En dimension 3 et en coordonnées cartésiennes, la divergence d'un champ de vecteurs
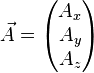
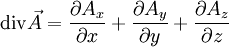
Formellement, l'opérateur divergence appliqué à un champ vectoriel
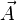

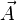
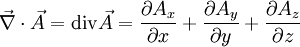
Cette définition a le désavantage d'être dépendante du choix d'une base orthonormée.
Définition en fonction d'une forme volume
Etant donnée une forme volume Ω sur un ouvert U de

![\mathrm d\left[\iota(X)\Omega\right]=\left(\operatorname{div} X\right)\Omega](https://static.techno-science.net/illustration/Definitions/autres/0/08631e82981b94dc97cfa13aa6f584ff_4a0c2139a28c0a64e99e82f3f28955e7.png)
Dans cette égalité, ι(X)Ω désigne le produit intérieur de Ω par le champ X ; c'est une n − 1 forme différentielle. Sa dérivée extérieure
![\mathrm d\left[\iota(X)\Omega\right]](https://static.techno-science.net/illustration/Definitions/autres/2/20327446df8d4f0c29f36afc0762ef39_c13bc8e272f7d8b43d8b2ad3a71031b4.png)
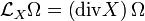
où
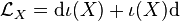

Si le champ X est intégrable, il définit un flot
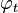
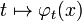
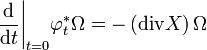
En particulier, le flot de X conserve le volume (c’est-à-dire
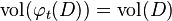
Définition en géométrie Riemannienne
Pour le volume de Lebesgue, la divergence de X s'exprime explicitement
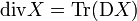
Ici, le champ X est considéré comme une application de U dans

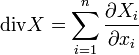
Le commentaire qui suit nécessite de connaitre la définition des connexions de Koszul et quelques notions de base en géométrie Riemannienne. Si g est une métrique riemannienne, alors, pour le volume Riemannien, la divergence de X est encore donnée par l'égalité (4), où D s'interprète comme la connexion de Levi-Civita associée à g.
Définition en termes de flux
La divergence peut être définie en termes de flux d'un champ de vecteur. Si D est un domaine régulier relativement compact de U, de bord S, le flux de X à travers S est égal à l'intégrale sur D de la divergence, d'après le théorème de Stokes. Explicitement,
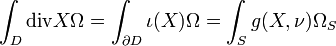
Dans la dernière intégrale, ν est le vecteur unitaire normal sortant de S, et ΩS est la forme volume sur l'hypersurface S. Cette égalité est valable en toute dimension pour des variétés riemanniennes orientées. Cette égalité est connue sous le nom de « théorème de Green-Ostrogradski » ou « théorème de flux-divergence ».
Une interprétation voisine est la suivante. Soit φt le flot du champ
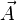
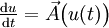
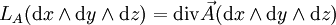
(on a désigné par LA l'opérateur dérivée de Lie ; pour les détails et un énoncé plus général, voir opérateur de Laplace-Beltrami).

















































