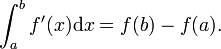Théorème de Stokes - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Articles d'analyse vectorielle | |

| |
| Objets d'étude | |
| Champ vectoriel | Champ scalaire |
| Équation aux dérivées partielles | |
| de Laplace | de Poisson |
| Opérateurs | |
| Nabla | Gradient |
| Rotationnel | Divergence |
| Laplacien scalaire | Bilaplacien |
| Laplacien vectoriel | D'alembertien |
| Théorèmes | |
| de Green | de Stokes |
| de Helmholtz | de flux-divergence |
| du gradient | du rotationnel |
En géométrie différentielle, le théorème de Stokes est un résultat central sur l'intégration de formes différentielles, qui généralise nombre de théorèmes sur l'analyse vectorielle. Après l'énoncé et la démonstration, cet article en propose nombre d'applications : en particulier, il fournit un formulaire qu'utilisent volontiers physiciens et ingénieurs, particulièrement en mécanique des fluides.
Théorème de Stokes — Soit M une variété différentielle orientée de dimension n, et ω une (n-1)-forme différentielle à support compact sur M de classe C1. Alors, on a :
où d désigne la dérivée extérieure,
Le théorème est attribué à Sir George Gabriel Stokes, mais le premier à connaître ce résultat est en réalité William Thomson. Le mathématicien et le physicien entretiennent une correspondance active durant 5 ans de 1847 à 1853.
La preuve demande de disposer d'une bonne définition de l'intégration ; il faut se rendre compte que l'apparente simplicité de la démonstration actuelle est trompeuse.
Démonstration
L'idée est d'utiliser une partition de l'unité adaptée au problème dans la définition de l'intégrale d'une forme différentielle ; et de se ramener à un cas presque évident.
Soit {Ui}I un recouvrement localement fini de M par des domaines de cartes locales
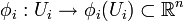
Introduisons fi une partition de l'unité subordonnée à {Ui}. Comme le support de ω est fermé, la forme différentielle ω s'écrit :
où la sommation est à support fini. Posons
![\beta_i=\phi_i^*\left[f_i\omega\right]](https://static.techno-science.net/illustration/Definitions/autres/0/0e09353643688c43fff332f6cfc42c37_cdc8ba2e88c92d6111f9dac82eda2022.png)
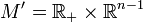
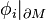
Comme
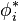
Par sommation, le théorème de Stokes est démontré une fois établi le cas particulier
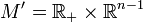
Une (n-1)-forme ω sur
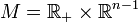
où le chapeau désigne une omission. On trouve alors :
Le théorème de Fubini donne :
L'hypothèse que la forme ω est à support compact permet alors de finir le calcul, car les termes
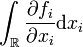
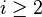
D'où le résultat.
Formule de Green-Riemann
Soit U un domaine compact lisse de
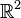
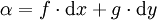
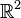
La formule de Green-Riemann est utilisée en géométrie pour démontrer l'inégalité de Poincaré.
Théorème fondamental de l'intégration
Si f est une fonction
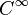
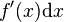
En fait, le théorème de Stokes est la généralisation de cette formule aux dimensions supérieures. La difficulté se trouve bien davantage dans la mise en place du bon cadre (formes différentielles, variétés à bord ou éventuellement plus générales, orientations) que dans la démonstration, qui repose sur le théorème fondamental de l'intégration et un argument de partition de l'unité.
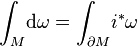
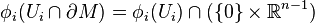
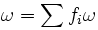
![\int_{\partial M}\!\left[f_i\omega\right]=\int_{\partial M'}\! \beta_i](https://static.techno-science.net/illustration/Definitions/autres/e/e16091ed5c99ef3406320172fa7fceeb_f5b46d1b0fa4535c1c6763a91e1eedd1.png)
![\int_M\! \mathrm d\left[f_i\omega\right]=\int_{M'}\! \mathrm \mathrm d\beta_i](https://static.techno-science.net/illustration/Definitions/autres/a/a000b57259b9d3555b59d982207733af_80cf5892cddce032eb3303debbc70fcd.png)
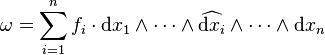
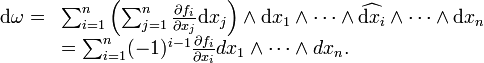
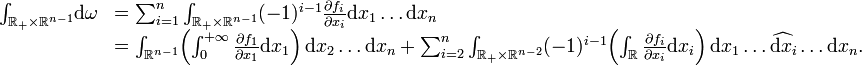
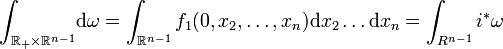
![\int_{\partial U} \alpha = \int_{\partial U}\! \left[f\cdot \mathrm dx+g\cdot \mathrm dy\right]=\iint_U \left[\frac{\partial g}{\partial x} -\frac{\partial f}{\partial y}\right] \,\mathrm dx\,\mathrm dy](https://static.techno-science.net/illustration/Definitions/autres/5/582d7002d0afb5e6f621b80297956397_a2f267c4be3fcd549ae38877675dfaeb.png)