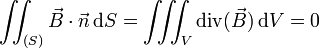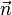Divergence (analyse vectorielle) - Définition

Utilisation en physique

Lois de conservation

Illustration représentant un volume V intérieur à la surface fermée (S) dont la normale extérieure en tout point est .

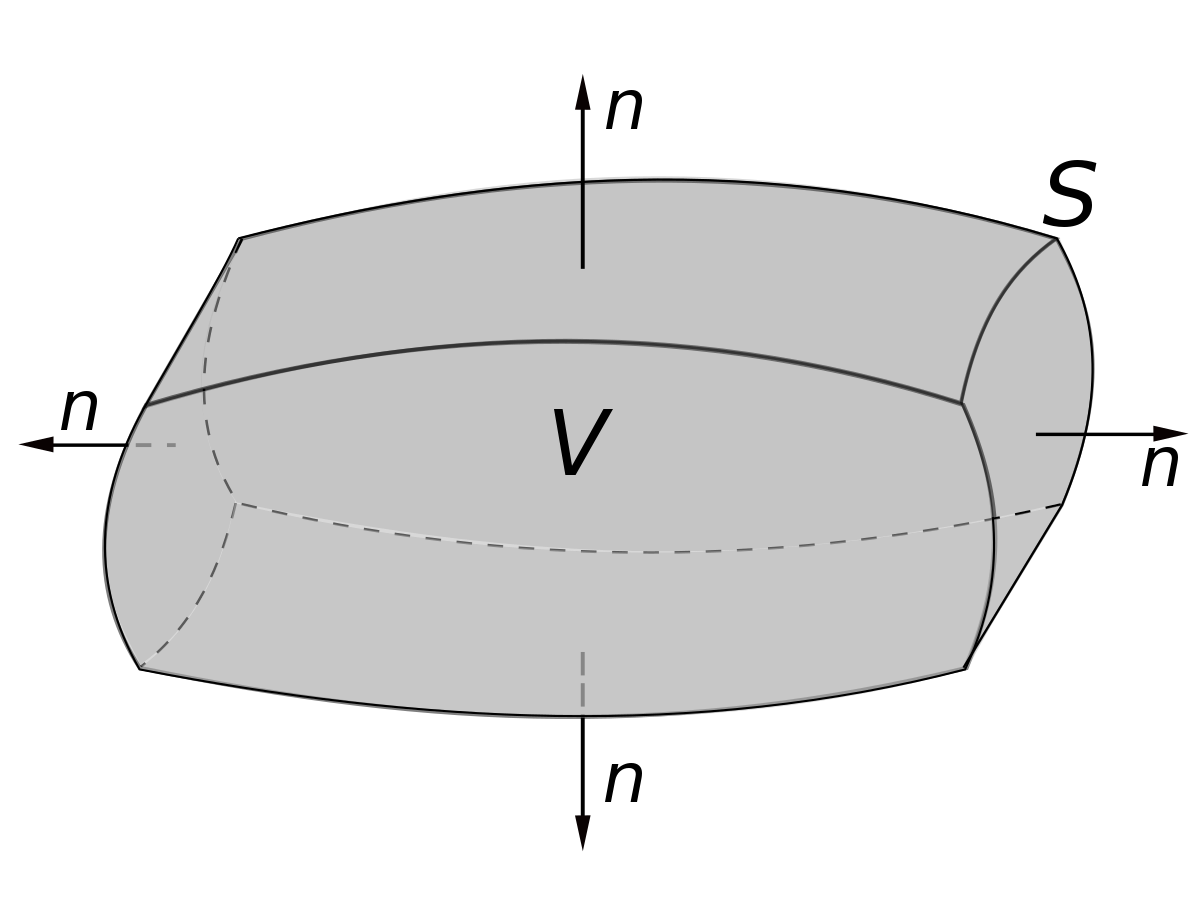
D'une manière générale, la divergence est reliée en physique à l'expression locale de la propriété de conservation d'une grandeur. En considérant une surface fermée quelconque (S), la variation d'une grandeur conservative dans le volume fermé par cette surface est, par définition d'une grandeur conservative, due aux échanges avec l'extérieur (il n'existe pas de sources de création ou d'annihilation d'une grandeur conservative). Le bilan de cette grandeur entre deux instants s'écrit donc uniquement comme la somme du flux de cette grandeur à travers la surface fermée (S) et de la variation temporelle de la grandeur à l'intérieur de la surface (S). Si la grandeur est conservative, ce bilan est nul.

Par exemple, en électromagnétisme, si est le vecteur densité volumique courant,ρ la densité volumique de charge électrique et V le volume intérieur à la surface (S), la conservation de la charge s'écrit de façon intégrale :

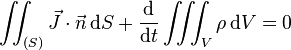
ou encore, pour une surface (S) fixe :

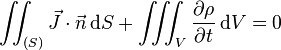
avec est un vecteur unitaire normal en tout point à (S).

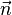
La formule d'Ostrogradsky permet de réécrire l'équation précédente en termes de divergence :

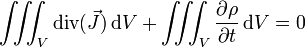
Ce qui mène immédiatement à la relation locale de conservation :

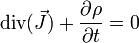
Il est ainsi également possible d'exprimer localement, par exemple dans le cadre de la mécanique des fluides, si ρ est la masse volumique en un point et le champ des vecteurs vitesse :

(équation de continuité).

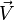
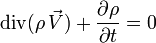
D'autres lois de conservation font intervenir la divergence de tenseurs d'ordre 2, comme la conservation de la quantité de mouvement en mécanique des fluides. En relativité générale, on montre aussi la nullité de la divergence du tenseur énergie-impulsion.

Champs radiaux en carré inverse de la distance

Lorsqu'une loi d'interaction radiale, due à des sources ponctuelles, varie comme le carré inverse de la distance il est possible d'établir que le flux du champ d'interaction à travers une surface fermée est toujours proportionnel à la quantité de sources présentes à l'intérieur de la surface fermée. Ce type de relation porte généralement en physique le nom de théorème de Gauss. Par exemple, dans le cas du champ électrostatique , dû aux charges électriques Q_int présentes à l'intérieur de la surface fermée (S) on a la forme intégrale du théorème de Gauss suivante :

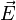
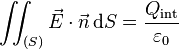
Grâce au théorème de flux-divergence il est possible d'exprimer une forme locale du théorème de Gauss. L'équation précédente se réécrit :

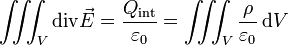
si V est le volume délimité par (S) et ρ la densité volumique de charge. On obtient alors immédiatement :

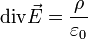
qui est la forme locale du théorème de Gauss. Ce type de relation est également possible pour le champ de gravitation :

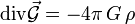
où G est la constante fondamentale de la gravitation, le champ de gravitation et ρ la masse volumique.

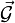
Flux du champ magnétique

En électromagnétisme il est possible de montrer, à partir de la loi de Biot et Savart, que la divergence du champ magnétique est nulle :

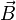
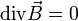
Cette propriété intrinsèque du champ magnétique permet d'établir que le flux du champ magnétique à travers une surface fermée est toujours nul ; on dit que le champ magnétique est à flux conservatif. En effet, si on appelle (S) la surface fermée considérée et V le volume intérieur à cette surface, on a :