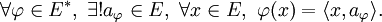Forme linéaire - Définition

Formes linéaires continues sur un espace de Hilbert

On suppose désormais que E est un espace de Hilbert sur le corps et on note le produit scalaire sur cet espace vectoriel.

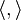
On démontre grâce au théorème de représentation de Riesz que les formes linéaires continues sur E s'expriment alors toutes d'une manière simple en fonction du produit scalaire et plus précisément :

Formes linéaires continues

Si on considère un espace vectoriel normé E sur le corps ou , alors on sait définir la notion de continuité de n'importe quelle application linéaire et en particulier, on dispose d'une notion de continuité pour les formes linéaires.

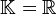
• Si E est un espace vectoriel normé et est une forme linéaire continue alors elle est uniformément continue.