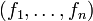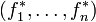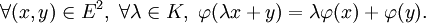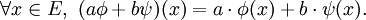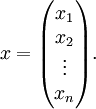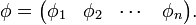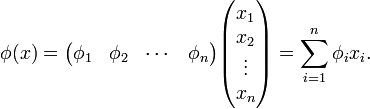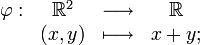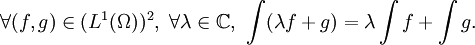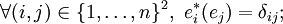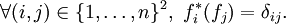Forme linéaire - Définition

Introduction

En algèbre linéaire, les formes linéaires désignent un type particulier d'applications linéaires. L'étude spécifique qu'on leur accorde est motivée par le fait qu'elles jouent un rôle primordial en mathématiques, et en analyse, par exemple dans la théorie des distributions, ou dans l'étude des espaces de Hilbert.

Les formes linéaires sur un espace vectoriel portent parfois également le nom de covecteur. Ce terme qui prend sens dans le cadre général des tenseurs et du calcul tensoriel rappelle que si les formes linéaires peuvent être représentées par un système de coordonnées comparable à celui des vecteurs, elles s'en distinguent pour ce qui est des formules de transformations.

Définition

Une forme linéaire sur un espace vectoriel E sur un corps K (ou covecteur de E) est une application linéaire définie sur E et à valeurs dans K.

En d'autres termes, on dit que l'application de E dans K est une forme linéaire si :

Espace dual

L'ensemble des formes linéaires sur E est lui-même un K-espace vectoriel. On l'appelle le dual de E et il est noté E ^* ou hom(E,K). Ainsi, si φ et ψ sont des formes linéaires et a et b des éléments de K :

L'application constante de valeur 0_K s'appelle la « forme linéaire nulle ».

On note parfois (où ) pour φ(x). Cette notation est appelée crochet de dualité.

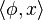
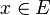
Représentations matricielles

Une base de E étant donnée, les composantes d'un vecteur sont ordonnées sous forme de vecteur colonne :

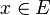
Au contraire, une forme linéaire ou covecteur est représentée par un vecteur ligne à n composantes :

Le crochet de dualité est le produit matriciel

Selon la convention d'Einstein, ce résultat peut se noter et est un scalaire (en réalité une matrice (1,1)).

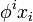
Exemples

• L'application

est une forme linéaire sur

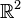
• Si L¹(Ω) est le -espace vectoriel des fonctions à valeurs complexes qui sont intégrables sur l'espace mesuré Ω, alors l'intégrale est une forme linéaire sur L¹(Ω). Cela signifie que

Propriétés algébriques

• Si est une forme linéaire non nulle, alors elle est surjective. On a donc .
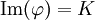
• Si est une forme linéaire non nulle, alors son noyau est un hyperplan de E.

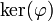
Réciproquement, si H est un hyperplan de E, il existe une forme linéaire telle que  ; cette forme linéaire (nécessairement non nulle) est unique, à un coefficient multiplicatif non nul près.

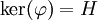
• Enfin, une propriété importante est que deux formes linéaires ont le même noyau si et seulement si elles sont proportionnelles.

Base duales et antéduales

L'ensemble des formes linéaires sur un espace vectoriel E est lui même un espace vectoriel et se note en général E ^* .Il est appelé espace vectoriel dual de E, ou plus simplement espace dual de E. Si E est de dimension finie n, il est remarquable que E ^* soit aussi de dimension finie n. En d'autres termes, on peut aussi dire qu'un espace de dimension finie est isomorphe à son dual. Cependant, il n'y a pas d'isomorphisme canonique dans le sens où si E est quelconque, il est nécessaire de se donner une base arbitraire afin de pouvoir définir un isomorphisme le reliant à E ^* . Si une base de E, on définit sur celle-ci les formes linéaires notées par :

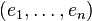
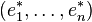
(où δ_ij est le symbole de Kronecker, c'est-à-dire valant 1 si i = j et 0 sinon).

Ces formes linéaires sont aussi appelées les projections des coordonnées, l'image d'un vecteur x par n'est autre que la i-ème coordonnée du vecteur x dans la base . Le résultat important est que la famille de formes linéaires forme une base de E ^* ; on appelle aussi cette base la base duale de la base .

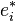
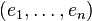
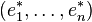
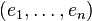
Inversement, si on se donne une base de E ^* , il existe une unique base de E telle que:

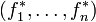
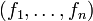
La base s'appelle la base antéduale de la base .