Espace vectoriel normé - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un espace vectoriel normé est une structure mathématique qui développe des propriétés géométriques de distance compatible avec les opérations de l'algèbre linéaire. Développée notamment par David Hilbert et Stefan Banach, cette notion est très importante en analyse et plus particulièrement en analyse fonctionnelle avec l'utilisation d'espaces de Banach tels que les espaces Lp ou les espaces de Sobolev Wk, p.
Structure générale
Définition formelle
Soit K un corps muni d'une valeur absolue, et non discret (par exemple le corps des réels ou des complexes).
Définition — Un K-espace vectoriel E est dit normé E lorsqu'il est muni d'une norme, c'est-à-dire d'une application
satisfaisant les hypothèses suivantes :
- séparation :
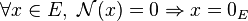
- homogénéité :
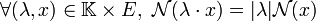
- sous-additivité :
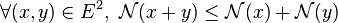
S'il n'y a pas de risque d'ambiguïté, la norme d'un élément x est notée
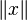
La boule unité (fermée) de E est l'ensemble des vecteurs de norme inférieure ou égale à 1.
Sous-espace et espace produit
Tout sous-espace vectoriel d'un espace vectoriel normé est normé par la restriction de la norme.
Soit (E, NE) et (F, NF) deux espaces vectoriel normés, alors l'application NExF définie par l'égalité suivante est une norme sur l'espace vectoriel produit ExF :

Espace quotient
Soit F un sous-espace vectoriel de E un espace vectoriel normé. On définit l'application
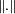

où d est la distance sur E (et sur ses parties) induite par la norme.
Cette application est manifestement homogène. Elle est de plus sous-additive, en effet :

est majoré par

Par défaut, l'espace vectoriel quotient est donc équipé d'une semi-norme. C'est une norme si et seulement si d(x,F)=0 implique que la classe de x est nulle, donc si et seulement si F contient son adhérence, c'est-à-dire F est fermé.
Propriété — Le quotient E/F muni de l'application
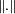
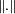
Exemples fondamentaux
Soit X un espace mesuré.
L'espace Lp(X) des fonctions p-intégrables sur X presque partout définies à valeurs réelles ou complexes, muni de la norme p associée, ainsi que l'espace L∞(X) des fonctions presque partout définies et bornées sur X à valeurs réelles ou complexe, muni de la borne supérieure essentielle du module, sont des espaces vectoriels normés.
- Si X est un segment de


- si X est un ensemble fini
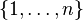
- si X est l'ensemble des entiers naturels muni de la mesure de comptage, on obtient les espaces de suites p-sommables
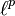
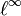
Explicitement,
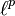


Remarque. Dans ces exemples, il n'est pas trop difficile de vérifier que la norme 1 ou
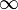
Cas particuliers
Espace préhilbertien
Un espace est dit préhilbertien s'il dispose d'une norme dérivée d'un produit scalaire, sans être nécessairement complet. (Un espace préhilbertien complet est un espace de Hilbert).
Ce type d'espace se caractérise par le fait qu'un tel E est isométriquement isomorphe à un sous-espace dense de son dual topologique. D'après la caractérisation mentionnée plus haut, ce dual, puisqu'il est complet, est donc isomorphe au complété de E.
Il existe une autre manière de caractériser un espace préhilbertien. Toute norme vérifiant l'identité du parallélogramme dérive d'un produit scalaire. Cette propriété est démontrée dans l'article Espace euclidien pour le cas réel et étendue dans le cas complexe dans l'article Espace hermitien.
Dimension finie
Soit E un espace vectoriel de dimension finie n sur le corps K des réels ou des complexes.
- Toutes les normes sur E sont équivalentes (donc définissent la même topologie).
- Cette topologie sur E est la seule qui en fasse un espace vectoriel topologique séparé.
- Pour toute norme sur E,
- toute application linéaire de E dans un espace vectoriel normé quelconque est (uniformément) continue,
- en particulier, E est (uniformément) homéomorphe à Kn;
- E est complet (c'est donc un espace de Banach) ; en particulier, tout sous-espace E de dimension finie d'un espace vectoriel normé F sur K de dimension quelconque est fermé dans F ;
- les parties compactes de E sont les fermés bornés ;
- la boule unité fermée de E est compacte.


















































