Produit scalaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie vectorielle, le produit scalaire est une opération algébrique s'ajoutant aux lois s'appliquant aux vecteurs. À deux vecteurs elle associe leur produit, qui est un nombre (ou scalaire). Elle permet d'exploiter les notions de la géométrie euclidienne traditionnelle : longueurs, angles, orthogonalité en dimension deux et trois, mais aussi de les étendre à des espaces vectoriels réels de toute dimension, et aux espaces vectoriels complexes.
Comme il existe deux grandes manières de définir les vecteurs, soit par une approche purement algébrique (cf espace vectoriel), soit par une approche géométrique à l'aide des bipoints (ou couple ordonné de points, cf Vecteur), il existe de même deux manières de présenter le produit scalaire : une manière algébrique, (objet de l'article Espace préhilbertien) et une manière géométrique, à l'aide de bipoints.
L'objectif de cet article est de présenter le produit scalaire de manière géométrique dans un espace euclidien traditionnel et de montrer comment cette notion peut s'étendre à tout espace vectoriel.
Aperçu des applications du produit scalaire
Le produit scalaire possède de multiples applications. En physique, il est, par exemple, utilisé pour modéliser le travail d'une force. En géométrie analytique il permet de déterminer le caractère perpendiculaire de deux droites ou d'une droite et d'un plan. Ce domaine est le sujet de cet article. Dans le cas de la dimension finie quelconque, il dispose de nombreuses applications algébriques : il permet de classifier les quadriques, offre des outils pour la réduction d'endomorphismes ou encore est à la base de multiples techniques statistiques comme la méthode des moindres carrés ou l'analyse en composantes principales. En géométrie, il confère à l'espace vectoriel une structure d'espace métrique disposant de nombreuses propriétés comme la complétude. Ces applications sont traitées dans les articles Espace euclidien et Espace hermitien. Le produit scalaire est aussi utilisé dans des espaces de dimension infinie, il permet alors de résoudre des équations aux dérivées partielles. La théorie devient plus subtile et de nombreux résultats, vrais en dimension finie, prennent une autre forme. Cet aspect du produit scalaire est traité dans les articles Espace préhilbertien et Espace de Hilbert.
Enfin, l'article géométrie euclidienne propose une synthèse de l'histoire, des implications et applications du produit scalaire en dimension finie.
Définitions et premières propriétés
Dans cette section, on considèrera un espace traditionnel tel qu'il est défini par Euclide : plan ou espace formé de points dans lequel les notions de distance et d'angle sont connues. On sait aussi calculer le cosinus de tout angle géométrique. Sont également utilisables le théorème de Pythagore, celui d'Al-Kashi et le théorème de Thalès. La construction géométrique des vecteurs dans un tel espace est détaillée dans l'article Vecteur.
Soient deux vecteurs représentés par des bipoints de mêmes origines (O, A) et (O, B). De tels représentants existent quel que soit le choix des vecteurs. Dans le reste de l'article, la longueur du bipoint (O, A) est notée OA ou parfois |OA|, c'est donc un nombre réel positif.
- Définition :
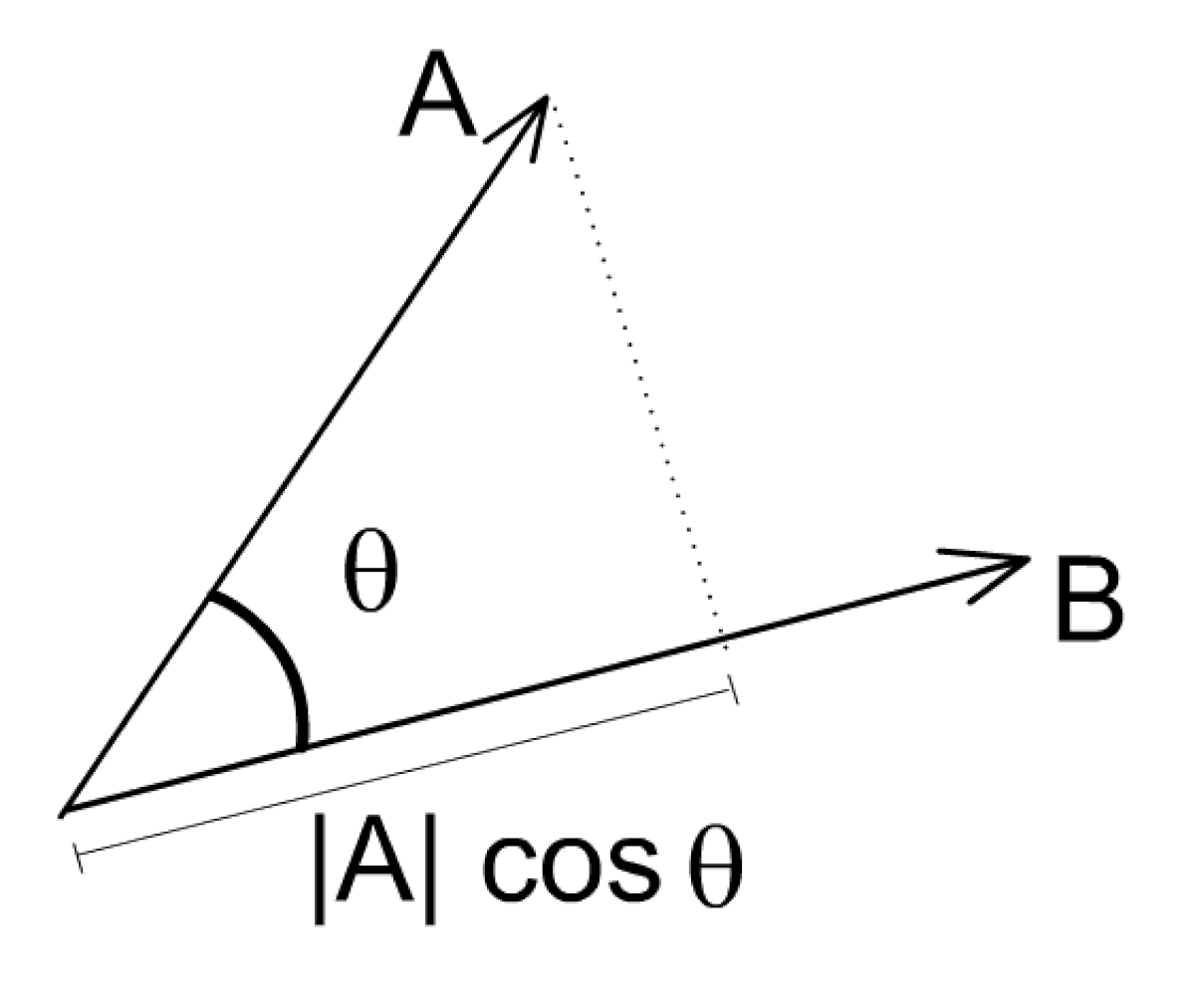
- Etant donnés des points O, A et B, on considère les vecteurs représentés par les bipoints OA et OB.
- Lorsque ces vecteurs sont non nuls le produit scalaire est le nombre réel OA·OB·cos(θ) où θ représente l'angle orienté AOB.
- Si l'un des vecteurs est nul alors le produit scalaire est nul.
- Dans tous les cas, on note ce produit scalaire :
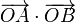
Dans le cas où aucun des vecteurs n'est nul, cette définition prend la forme suivante :
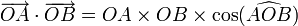
Ici cos désigne la fonction mathématique cosinus et

Dans le cas où les deux vecteurs sont égaux, la notation suivante est utilisée :
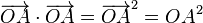
La valeur du produit scalaire correspond alors à l'aire d'un carré de côté OA.
- Définition :
- La norme euclidienne d'un vecteur représenté par un bipoint AB est la distance qui sépare A de B. En général, elle est notée
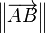
- Elle est égale à la racine carrée du produit scalaire du vecteur avec lui-même.
![\left\| \overrightarrow {AB} \right\| = \sqrt[]{\overrightarrow {AB}\cdot\overrightarrow {AB}}](https://static.techno-science.net/illustration/Definitions/autres/f/f86ba421646aa922511015ee1522f466_c45aa338cc20475a6fd37f7b6d3d91c7.png)
Une inégalité évidente est vérifiée par le produit scalaire ainsi défini :
- Inégalité de Cauchy-Schwarz
- Soient O, A et B trois points du plan, la valeur absolue du produit scalaire des deux vecteurs d'extrémités O, A et O, B est toujours inférieure ou égale au produit des normes des deux vecteurs. Cette majoration s'écrit :
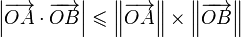
L'égalité a lieu si et seulement si les trois points sont alignés. Cette majoration provient du fait que la fonction cosinus prend ses valeurs dans l'intervalle d'extrémité 1 et -1. Pour que l'égalité ait lieu, il faut et il suffit que le cosinus ait pour valeur soit 1 soit -1, c'est-à-dire que l'angle soit nul ou plat. Ce qui signifie bien que les trois points sont alignés. Une fois encore, cette inégalité est l'objet de l'article Inégalité de Cauchy-Schwarz, l'article suppose encore une formalisation algébrique différente de celle choisie ici.

















































