Formules pour les nombres premiers - Définition

Formules approchées

Des formules approchées donnant le n-ème nombre premier p_n, ou le nombre de nombres premiers , π(n), ont été imaginées au 18^ème siècle, culminant avec les conjectures de Legendre et Gauss. Si leur hypothèse la plus simple, a été démontré par Hadamard et de la Vallée Poussin un siècle plus tard (c'est le théorème des nombres premiers), la difficulté du problème est bien montrée par le fait qu'une des conjectures de Gauss, plus précise, et majorant π(n) par , qui paraissait fort plausible au vu des tables de ces deux fonctions, s'est cependant avérée fausse, mais seulement pour des valeurs de n gigantesques.

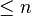
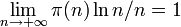
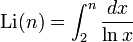
Des résultats plus précis, et en particulier une bonne estimation du terme d'erreur h(n) dans la formule p_n = nlnn + h(n), font encore l'objet de conjectures (dépendant souvent de l'hypothèse de Riemann) ; parmi les meilleurs résultats vraiment démontrés, on peut citer l'encadrement suivant, déterminé par Dusart en 1999 :

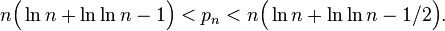
Ces méthodes sont loin de donner des formules exactes ; par exemple, cet encadrement affirme seulement que le millième nombre premier, 7919, est compris entre 7840 et 8341.