Formules pour les nombres premiers - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la recherche de formules exactes donnant tous les nombres premiers (ou même donnant uniquement des nombres premiers) s'est généralement avérée vaine, ce qui a amené à se contenter de formules approchées. Cette page recense les différents résultats obtenus.
Formules exactes simples
Le rêve d'une formule exacte et simple donnant le n-ème nombre premier pn, ou le nombre de nombres premiers
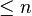
C'est ce qui explique l'intérêt de la remarque d'Euler : le polynôme quadratique
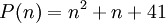
D'autres formules utilisant des fonctions plus générales, telle celle de Mersenne, avaient été envisagées, la plus célèbre étant celle conjecturée par Fermat :
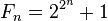
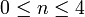
Des formules exactes... mais sans intérêt pratique
Malgré les remarques précédentes, il est cependant possible d'obtenir des formules exactes d'apparence simple. Ainsi, le théorème de Wilson permet facilement de montrer que la fonction
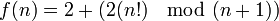
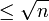
D'autres formules donnant directement pn ou π(n) peuvent été construites à partir de f ; ainsi, on a, en utilisant la fonction partie entière :
-
![\pi(m) = \sum_{j=2}^m \left[ {(j-1)! + 1 \over j} - \left[{(j-1)! \over j}\right] \right]](https://static.techno-science.net/illustration/Definitions/autres/9/9421124553f30b14c20a2f92cce5a104_0037bd963574e4b9ad3c23e9ce3ebdf7.png)
mais ces formules sont, bien évidemment, encore moins utilisables que celle donnant f.
Une autre approche, plus prometteuse et n'utilisant pas le théorème de Wilson, consiste essentiellement à "simuler" le crible d'Ératosthène, ou les formules qu'on peut en déduire, comme la formule d'inclusion-exclusion de Legendre ; c'est le terrain de prédilection de nombreux amateurs, ainsi, les formules suivantes ont été déterminées en 2000 par un enseignant espagnol, S.M.Ruiz :
et
on remarquera le nombre important de sommations dans ces formules, qui fait qu'elles seraient, elles aussi, peu utilisables en pratique ; de bien meilleures méthodes de calcul exact de π(n) et pn, qu'on trouvera détaillées dans l'article consacré à ces fonctions, restent d'ailleurs relativement inefficaces.
Compte tenu des remarques de la première section, l'existence de polynômes à plusieurs variables ne prenant que des valeurs premières paraissait peu vraisemblable, aussi les travaux de Matiyasevich (en 1970), montrant que toute relation diophantienne pouvait être "codée" par un tel polynôme, provoquèrent une véritable surprise. Il est même possible de donner des exemples explicites de ce résultat ; ainsi, le monstrueux polynôme suivant (comportant 26 variables, et de degré 25):
- (k+2)[1 – (wz+h+j–q)2 – [(gk+2g+k+1)(h+j) + h – z]2– (2n+p+q+z–e)2 – [16(k+1)3(k+2)(n+1)2 + 1 – f2]2– [e3(e+2)(a+1)2 + 1 – o2]2 – [(a2–1)y2 + 1 –x2]2– [16r2y4(a2–1) + 1 – u2]2
– [((a+u2(u2–a))2–1)(n+4dy)2 + 1 – (x+cu)2]2 –[n+l+v–y]2– [(a2–1)l2 + 1 – m2]2 – [ai+k+1–l–i]2 – [p + l(a–n–1) + b(2an+2a–n2–2n–2) – m]2 – [q+ y(a–p–1) + s(2ap + 2a – p2 – 2p – 2) – x]2
-
- – [z + pl(a–p) + t(2ap – p2 – 1) – pm]2]
a, pour ensemble de valeurs positives, exactement l'ensemble des nombres premiers. Mais on peut commencer à se demander s'il s'agit bien encore là de "formules" ; dans un ordre d'idées assez proche, Conway a défini une généralisation du problème de Syracuse, qui le transforme en un langage de programmation, FRACTRAN ; le texte suivant :
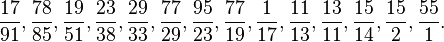
correspond, pour ce langage, à un programme qui produit, dans l'ordre, la suite des nombres premiers, ce qui peut être considéré comme une formule au moins aussi élégante que celles qui précédent.
Enfin, Mills a montré qu'il existe des nombres réels M tels que pour tout entier n, la partie entière de
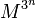
![p(n)=\left[M^{3^n}\right]](https://static.techno-science.net/illustration/Definitions/autres/b/b6b9a1db1d471ceeb474c8086655ded7_19c4f7b0d365491ec7bdb740cb9e6704.png)
![\pi(k) = k - 1 + \sum_{j=2}^k \left[ {2 \over j} \left(1 + \sum_{s=1}^{\left[\sqrt{j}\right]} \left(\left[{ j-1 \over s}\right] - \left[{j \over s}\right]\right) \right)\right]](https://static.techno-science.net/illustration/Definitions/autres/2/2da2a73fdb5e8f6b730445b866778593_807d595b61835297331cc14ec87fedfd.png)
![p_n = 1 + \sum_{k=1}^{2([ n \ln(n)]+1)} \left(1 - \left[{\pi(k) \over n} \right]\right).](https://static.techno-science.net/illustration/Definitions/autres/8/8bfe568062006c02c03d6fc5b09b78c1_602abe3adca9149586975abd6e9ee238.png)