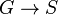Groupe algébrique - Définition

Exemples

• Si Γ est un groupe fini, il existe un unique groupe algébrique sur K tel que G(L) = Γ pour toute extension de corps L/K. C'est le groupe constant Γ.

• Le groupe additif G_a: la variété sous-jacente est la droite affine A^1 sur K. Pour toute K-algèbre de type fini A, le groupe G_a(A) s'identifie canoniquement au groupe (additif) A.

• Le groupe multiplicatif G_m: la variété sous-jacente est la droite affine A^1 sur K privée de l'origine. Pour toute K-algèbre de type fini A, le groupe G_m(A) s'identifie canoniquement au groupe multiplicatif A ^* des éléments inversibles de A.

• GL_n,K, le groupe des matrices inversibles, est un groupe algébrique. Pour toute K-algèbre de type fini A, le groupe GL_n,K(A) s'identifie au groupe multiplicatif des matrices carrés d'ordre n, à coefficients dans A et inversibles. Lorsque n=1, on retrouve le groupe multiplicatif G_m.

• Les courbes elliptiques sont des groupes algébriques.

• Soit n un entier naturel. La multiplication par n induit un homomorphisme de groupes algébriques . Si n est premier à la caractéristique du corps K, alors le noyau de cet homomorphisme est réduit à l'élément neutre.

• Si K est de caractéristique p positive, l'élevation à la puissance p (appelé le Frobenius) dans G_a est un homomorphisme de groupes algébriques. Son noyau, noté α_p, est un exemple typique de groupe algébrique non-lisse. La variété algébrique sous-jacente est Spec K[T] / (T^pK[T]) (elle n'a qu'un seul point et n'est pas réduite).

• Soit n un entier naturel. Dans le groupe multiplicatif G_m, l'élevation à la puissance n induit un homomorphisme de groupes algébriques, dont le noyau μ_n est un groupe algébrique fini, constant si le corps de base K contient toutes les racines n-ième de l'unité. Il est étale sur K si et seulement si n est premier à la caractéristique de K.

• En géométrie algébrique, un tore T sur K est un groupe algébrique, isomorphe à un produit de G_m sur la clôture algébrique de K. On dit que T est déployé si l'isomorphisme est défini sur K.

Deux classes de groupes algébriques sont particulièrement importantes. Tout d'abord, les variétés abéliennes sont des groupes algébriques pour lesquelles la variété sous-jacente est propre, connexe, et lisse. Les courbes elliptiques sont des exemples de variétés abéliennes.

Ensuite viennent les groupes algébriques linéaires : ceux-ci correspondent au cas où le groupe est une variété affine, autrement dit, où c'est le lieu des zéros d'une famille de polynômes dans . La plupart des sous-groupes usuels de GL_n(K) correspondent à des groupes algébriques linéaires. Par exemple, SL_n(K) est l'ensemble des zéros du polynôme det − 1. On peut montrer que les groupes algébriques linéaires peuvent être représentés fidèlement. Ainsi, ils peuvent toujours être vus comme des sous-groupes de GL_n,K, ce qui explique leur appellation.

Généralisation

Soit S un schéma. Un schéma en groupes sur S est un S-schéma qui représente un foncteur de la catégorie des S-schémas dans la catégorie des groupes.

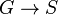
• Plus concrètement, on demande que pour tout S-schéma T, l'ensemble G(T) = Mor_S(T,G) soit un groupe et que pour tout , l'application canonique soit un morphisme de groupes.

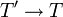
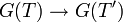
• Une autre façon de définir les schémas en groupes est de dire qu'il existe un morphisme (la multiplication), un automorphisme (l'inverse) et une section du morphisme structural (section neutre) qui vérifient les axiomes habituels d'un groupe.

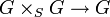
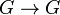
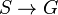
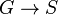
Si est de plus de type fini, alors pour tout , la fibre G_s est un groupe algébrique sur le corps résiduel k(s). Ainsi peut être vu comme une famille de groupes algébriques paramétrés par les points de S.

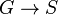
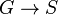
Les exemples standard de groupes algébriques G_a,G_m, courbes elliptiques etc se généralisent facilement en schémas en groupes sur une base S quelconque.

Un schéma en groupes est séparé sur S si et seulement si la section neutre est fermée dans G.