Groupe algébrique - Définition

Introduction

En géométrie algébrique, la notion de groupe algébrique est un équivalent des groupes de Lie en géométrie différentielle ou complexe. Un groupe algébrique est une variété algébrique munie d'une loi de groupe compatible avec sa structure de variété algébrique.

Définition

Un groupe algébrique sur un corps (commutatif) K est une variété algébrique G sur K munie :

• d'un morphisme de K-variétés algébriques (appelé aussi multiplication) . La variété source étant le produit fibré de G par lui-même;

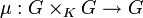
• d'un morphisme inverse ;

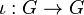
• d'un élément neutre ε appartenant à G(K) (un point rationnel de G)

vérifiant formellement les axiomes d'un groupe. Si G est réduit et si K est algébriquement clos, il suffit que ces morphismes induisent une structure de groupe sur l'ensemble G(K) des points rationnels de G.

Pour toute variété algébrique X sur K, l'ensemble G(X) des K-morphismes de X dans G hérite d'une structure de groupe. Une façon rapide de définir un groupe algébrique est alors de dire que c'est une variété algébrique qui représente un foncteur de la catégorie des variétés algébriques sur K dans la catégorie des groupes.

Attention : est muni de la topologie de Zariski et non de la topologie produit.

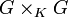
• Un homomorphisme de groupes algébriques sur K est un morphisme de variétés algébriques sur K qui est compatible avec la structure de groupe: si μ_G,μ_H sont les lois de multiplication sur G et H respectivement, alors . En termes des points, cela revient à dire que pour toute K-algèbre de type fini A, l'application induite par f est un homomorphisme de groupes. Si K est algébriquement clos et si G, H sont réduits, il suffit de prendre A=K.

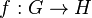
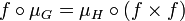
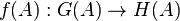
• Un isomorphisme de groupes algébriques est un homomorphisme de groupes algébriques qui est un isomorphisme pour les variétés algébriques sous-jacentes.

• Un sous-groupe algébrique F de G est une sous-variété de G telle que l'immersion soit un homomorphisme de groupes algébriques. On sait que F est alors une sous-variété fermée.

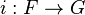
• Si est un homomorphisme de groupes algébriques sur K, le noyau Ker(f) de f est défini par . L'espace sous-jacent à Ker(f) est f ^{− 1}(ε_H), mais la structure de sous-variété n'est pas nécessairement réduite. On montre facilement que Ker(f) est un sous-groupe algébrique de G.

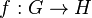
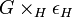
Structure

Structure de variété

Un groupe algébrique géométriquement réduit est automatiquement lisse. Sur un corps de caractéristique 0, tout groupe algébrique est lisse (théorème de Cartier). En revanche, si K est de caractéristique p positive, il existe des groupes algébriques non-lisses (voir l'exemple α_p ci-dessus).

Décomposition

Si G est un groupe algébrique sur un corps K, on peut décomposer G comme suit.

• Il existe un sous-groupe ouvert G⁰ de G, appelé la composante neutre de G, et un groupe algébrique π₀(G) fini étale sur K, tels que G soit extension de π₀(G) par G⁰, c'est-à-dire qu'on a une suite exacte

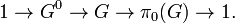
Si K est algébriquement clos, π₀(G) est un groupe fini constant.

• Supposons maintenant G lisse et K parfait (par exemple de caractéristique 0). Alors G⁰ est extension d'une variété abélienne par un groupe linéaire lisse L (théorème de Chevalley).

• Supposons de plus que G est commutatif. Le groupe linéaire L est produit d'un tore par un groupe unipotent (c'est-à-dire un groupe algébrique qui est extensions successives de G_a). En caractéristique 0, les groupes unipotents sont isomorphes à un produit de G_a.

Formes différentielles

Si G est un groupe algébrique lisse, alors son fibré tangent est constant, engendré par l'espace tangent de G à l'origine ε_G. Par dualité, le faisceau des formes différentielles sur G est libre (rappelons que sur une variété algébrique lisse, le faisceau des formes différentielles est seulement localement libre en général).