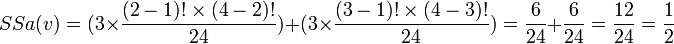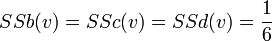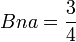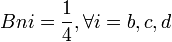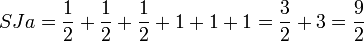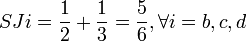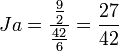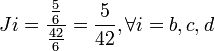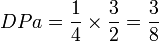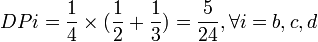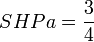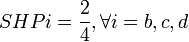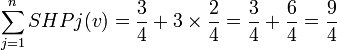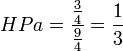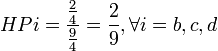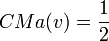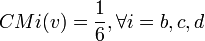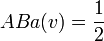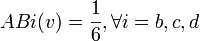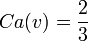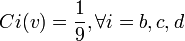Indices de pouvoir - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Introduction - Définitions, exemples et notations - Historique - Éléments de comparaison - Neuf indices de pouvoirs - Interprétation probabiliste des indices de pouvoirs - Postulats et paradoxes - Sources et références

Neuf indices de pouvoirs

La liste des indices suivante est non exhaustive, ne comprend pas certaines mesures trop similaires des indices présentés et ne recense pas les indices mesurant la satisfaction (plutôt que le pouvoir des votants).

Indice de Shapley-Shubick

Le premier indice de pouvoir est celui de Shapley-Shubik et il a été formulée par Lloyd Shapley et Martin Shubik en 1954. Il s'agit à l'origine de la Valeur de Shapley un concept de Théorie des jeux construit pour être appliqué aux jeux sous forme de fonction caractérisant la classe des jeux simples. Shapley et Shubik l'ont proposé comme une mesure de pouvoir a priori dans un processus de vote.
Principe: On considère un groupe d'individus votant l'amendement d'une loi selon la procédure qui suit:

ils votent chacun leur tour;
dès qu'une majorité est atteinte, l'individu qui a voté en dernier reçoit une "unité de pouvoir" (puisque l'amendement est passé grâce à sa voix).

Remarque n°1: L'invidu en question est décisif dans la coalition formée par lui-même et tous ceux qui le précèdent.

Idée de l'indice: Si l'on suppose que l'ordre dans lequel les individus prennent part au vote est déterminé de manière aléatoire et équiprobable, on peut déterminer le nombre moyen de fois où individu donné est décisif.

Formulation mathématique: L'indice de Shapley-Shubick pour le joeur $i$ :

$SSi(v) = \sum_{i\in S\geq N} \frac{(s-1)!(n-s)!}{n!} [v(S)-v(S-{i})]$

où $n!$ donne tous les ordres de passage possibles et v(S)-v(S-{i}) permet de repérer les fois où l'individu i est décisif.

Remarque n°2: Cette expression revient à diviser le nombre de permutations des joueurs pour lesquelles le joueur i est décisif par le nombre total de permutations possibles.

Remarque n°3: Comme toutes permutation comprend un et seul joueur décisif, cela implique que l'on a:

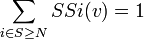
$\sum_{i\in S\geq N}SSi(v) =1$

En appliquant le principe de calcul de l'indice avec le tableau n°1, on obtient:

$SSa(v)= (3\times\frac{(2-1)!\times(4-2)!}{24}) + (3\times\frac{(3-1)!\times(4-3)!}{24}) = \frac{6}{24} + \frac{6}{24} = \frac{12}{24} = \frac{1}{2}$
$SSb(v) = SSc(v) = SSd(v) = \frac{1}{6}$

Indice de Banzhaf

John Francis Banzhaf III a proposé un indice qui diffère peu de celui de Shapley-Shubik. Son objectif était d'aider à résoudre certains débats juridiques concernant les normes d'équité constitutionnelles pour les systèmes de représentation électorale (Banzhaf voulait prouver objectivement que le système de vote au Conseil du Comté de Nassau était injuste). Banzhaf considère, comme Shapley et Shubik, que la mesure du pouvoir du joueur i doit dépendre du nombre de fois où il est décisif.

Toutefois le processus de décision de Banzhaf n'est pas séquentiel (il ne considérait pas qu'il fallait, comme dans le cas de Shapley-Shubik, un ordre d'arrivé): les coalitions votent bloc. Par conséquent le "score" de Banzhaf du joueur i est le nombre de coalitions possibles (et non le nombre de permutations possibles) pour lesquels i est décisif.

Le fonctionnement de l'indice de Banzhaf est très simple: on regarde le nombre de fois où un joueur est décisif et on divise par le nombre de fois où tous les joueurs sont décisifs.

Indice normalisé de Banzhaf: Pour un jeu (N,v) l'indice normalisé de Banzhaf du joueur $i$ est défini par:

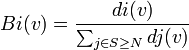
$Bi(v) = \frac{di(v)}{\sum_{j\in S\geq N} dj(v)}$

En reprenant à nouveau l'exemple 2, on observe que les joueurs sont décisifs 12 fois (la somme des 1 du tableau n°1 vaut 12), et d'où:

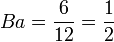
a = 6 fois décisifs $\rightarrow$ $Ba = \frac{6}{12} = \frac{1}{2}$
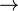
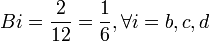
b = c = d = 2 fois décisifs $\rightarrow$ $Bi = \frac{2}{12} = \frac{1}{6}, \forall i = b,c,d$

Dubey et Shapley ont proposé une autre pondération du score de Banzhaf.
Indice de Banzhaf non normalisé: Pour un jeu (N,v) l'indice non normalisé de Banzhaf du joueur $i$ est défini par:

$Bni(v) = \frac{di(v)}{2^{n-1}} = \frac{1}{2^{n-1}}\times\sum_{i\in S\geq N} [v(S)-v(S-{i})]$

où le $2 n - 1$ est le nombre de coalition auquel appartient i.
Remarque n°1:Cette formulation de l'indice Banzhaf, que Dubey et Shapley justifient par des arguments probabilistes est la plus utilisée dans la littérature.
Remarque n°2: L'indice normalisé de Banzhaf est souvent associé au nom de Coleman et l'indice non normalisé trouve son origine dans les travaux de Penrose.

En reprenant l'exemple n°2, on a:

$Bna = \frac{3}{4}$
$Bni = \frac{1}{4} , \forall i = b,c,d$

Indice de Johnston

Johnstion propose une modification de la pondération de l'indice de Banzhaf, en considérant que la mesure du pouvoir devrait dépendre du nombre de joueurs décisifs dans une coalition donnée. L'idée est que moins il y a de joueurs décisifs dans une coalition plus le pouvoir d'un seul joueur décisif sera fort.

Dans un jeu (N,v), le score de Johnston du joueur $i$ est défini par:

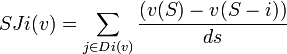
$SJi(v) = \sum_{j\in Di(v)} \frac{(v(S)-v(S-{i}))}{ds}$

où ds est le nombre de pivôt dans la coalition.

Indice de Johnston: Pour un jeu (N,v), l'indice de Johnston du joueur $i$ est:

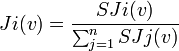
$Ji(v) = \frac{SJi(v)}{\sum_{j=1}^n SJj(v)}$

En reprenant l'exemple n°2, on a:

$SJa = \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + 1 + 1 + 1 = \frac{3}{2} + 3 = \frac{9}{2}$
$SJi = \frac{1}{2} + \frac{1}{3} = \frac{5}{6} , \forall i = b,c,d$

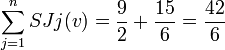
D'où: $\sum_{j=1}^n SJj(v) = \frac{9}{2} + \frac{15}{6} = \frac{42}{6}$

Et on obtient alors:

$Ja = \frac{\frac{9}{2}}{\frac{42}{6}} = \frac{27}{42}$
$Ji = \frac{\frac{5}{6}}{\frac{42}{6}} = \frac{5}{42} , \forall i = b,c,d$

Indice de Deegan-Packel

Deegan et Packel ont proposé un indice de pouvoir basé sur le principe de taille de Riker. Ce principe revient à considérer que seules se forment les coalitions minimales gagnantes. L'indice de Deegan-Packel est obtenu en supposant que seules les coalitions minimales gagnantes se forment de manière équiprobable et que chaque joueur d'une coalition minimale gagnante reçoit un "montant de pouvoir" inversement proportionnel à la taille de cette coalition.

Indice de Deegan-Packel: Pour un jeu (N,v), l'indice de Deegan-Packel du joueur $i$ est:

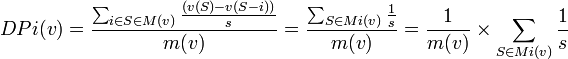
$DPi(v) = \frac {\sum_{i\in S\in M(v)} \frac{(v(S)-v(S-{i}))}{s}}{m(v)} = \frac {\sum_{S\in Mi(v)} \frac{1}{s}}{m(v)} = \frac {1}{m(v)}\times\sum_{S\in Mi(v)} \frac{1}{s}$

Ici:

$m (v)$ est le nombre de coalitions minimales gagnantes,
$M (v)$ la coalition minimale gagnante,
v(S)-v(S-{i}) indique lorsque i est pivot ( $\neq 0$ ).

En reprenant l'exemple n°2, à partir du tableau n°2 (vu que l'on se sert de coalitions minimales gagnantes), on a:

$DPa = \frac{1}{4} \times \frac{3}{2} = \frac{3}{8}$
$DPi = \frac{1}{4} \times (\frac{1}{2} + \frac{1}{3}) = \frac{5}{24} , \forall i = b,c,d$

Indice de Hollard-Packel

Hollard et Packel ont proposé une modification de l'indice de Deegan-Packel en supposant que tous les joueurs d'une coalition minimale gagnante reçoivent le même montant de pouvoir quel que soit la taille de la coalition. Il s'agit d'une redéfinition de l'indice de Deegan-Packel afin de prendre en compte les situations où la valeur associée à une coalition gagnante correspond à un bien collectif dont tout les membres de la coalition peuvent profiter sans exclusion ni rivalité (et non a un bien privée divisible): quand on prend une $m (v)$ , tout le monde a le même pouvoir (considéré comme un bien public non divisible).

Dans un jeu (N,v), le score de Hollard-Packel du joueur $i$ est:

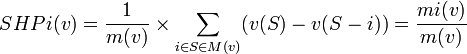
$SHPi(v) = \frac {1}{m(v)}\times\sum_{i\in S\in M(v)} (v(S)-v(S-{i}))= \frac {mi(v)}{m(v)}$

Indice de Hollard-Packel: Pour un jeu (N,v), l'indice de Hollard-Packel du joueur $i$ est:

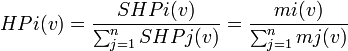
$HPi(v) = \frac{SHPi(v)}{\sum_{j=1}^n SHPj(v)} = \frac{mi(v)}{\sum_{j=1}^n mj(v)}$

En reprenant l'exemple n°2, on obtient:

$SHPa = \frac{3}{4}$
$SHPi = \frac{2}{4} , \forall i = b,c,d$

D'où:

$\sum_{j=1}^n SHPj(v) = \frac{3}{4} + 3 \times \frac{2}{4} = \frac{3}{4} + \frac{6}{4} = \frac{9}{4}$

Et:

$HPa = \frac{\frac{3}{4}}{\frac{9}{4}} = \frac{1}{3}$
$HPi = \frac{\frac{2}{4}}{\frac{9}{4}} = \frac{2}{9} , \forall i = b,c,d$

Indice de Curiel

Un nouvel indice, fondé sur le principe de taille de Riker(comme les indices de Deegan-Packel et Hollard-Packel), est proposé par Curiel. Dans cet indice, Curiel relâche l'hypotèse, bien qu'implicite, d'équiprobabilité d'occurrence ou de formation des coalitions minimales gagnantes. Curiel associe à chaque coalition $S\subset N$ , $S\neq \varnothing$ un poids $r s > 0$ qui représente une de la probabilité d'occurrence de la coalition S. 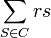Pour un ensemble de coalition C, on note $\sum_{S\in C} rs$ par r(C). 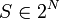Pour tout jeu simple (N,v) et toute coalition $S\in 2^N$ , la probabilité d'occurrence de la coalition S, ps(v), est définie par :

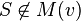
$p s (v) = 0$ si $S\not\in M(v)$ ,
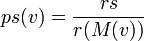
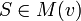
$ps(v)=\frac {rs}{r(M(v))}$ si $S\in M(v)$

Pour toute coalition S:

$p s (v) = 0$ ,
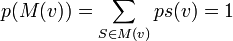
$p(M(v))=\sum_{S\in M(v)} ps(v)=1$

Dans un jeu (N,v), le score du Curiel du joueur $i$ est:

$\delta i(v) = \sum_{S\in Mi(v)} ps(v)$

Indice de Curiel: Pour un jeu (N,v), l'indice de Curiel du joueur $i$ est:

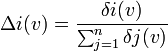
$\Delta i(v) = \frac{\delta i(v)}{\sum_{j=1}^n \delta j(v)}$

Remarque n°1: L'indice ne peut se calculer sans connaître les poids rs.
Remarque n°2: La première distribution de poids suggérée par Curiel revient à supposer l'équiprobabilité d'occurrence des coalitions minimales gagnantes. Dans ce cas l'indice de Curiel coïncide avec celui de Hollard-Packel.
Remarque n°3: Une seconde distribution de poids consiste à supposer que la probabilité d'occurrence d'une coalition est inversement proportionnelle à sa taille. Dans ce cas l'indice de Curiel est identique à celui de Deegan-Packel.

Indice de Colomer-Martinez

Un nouvel indice de pouvoir, également fondé sur le principe de taille de Riker, est proposé par Colomer et Martinez.
Ces derniers défendent l'idée selon laquelle un indice de pouvoir, dans le cadre bien défini de la genèse d'une coalition gouvernementale, à deux fonctions:

estimer la capacité d'un parti à faire basculer le résultat d'un vote,
mesurer le pouvoir de ce parti au sein des coalitions auxquelles il appartient.

Pour un jeu simple pondéré $v :[q; w 1,..., w n]$ , l'indice de Colomer-Martinez du joueur $i$ est:

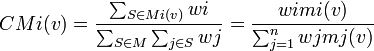
$CMi(v) = \frac {\sum_{S\in Mi(v)} wi} {\sum_{S\in M} \sum_{j\in S} wj} = \frac {wimi(v)} {\sum_{j=1}^n wjmj(v)}$

En reprenant l'exemple n°2, on obtient:

$CMa(v) = \frac{1}{2}$
$CMi(v) = \frac{1}{6} , \forall i = b,c,d$

Indice d'Andjiga-Berg

Deux chercheurs, Andjiga en 1996 et Berg en 1999, ont ,indépendamment l'un de l'autre, proposé un indice reposant sur les deux principes suivant:

Seules les coalitions gagnantes peuvent se former et ce de manière équiprobable.
Dans une coalition S un joueur i obtient une fraction de pouvoir qui est inversement proportionnelle à la taille de la coalition S tant que le joueur i est décisif dans S.

Le score d'Andjiga-Berg du joueur $i$ est donné par:

$SABi(v)=\frac {1}{g(v)}\times\sum_{S\in Gi(v)} \frac{1}{s}\times[v(S)-v(S-{I})]$

où g(v) désigne le nombre de coalitions gagnantes.
L'indice d'Andjiga-Berg du joueur $i$ est:

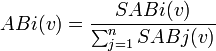
$ABi(v) = \frac {SABi(v)} {\sum_{j=1}^n SABj(v)}$

En reprenant l'exemple n°2, on obtient:

$ABa(v) = \frac{1}{2}$
$ABi(v) = \frac{1}{6} , \forall i = b,c,d$

Indice de Chakravarty

Chakravarty a proposé en 2000 ce dernier indice en suggèrant que le pouvoir absolu d'un joueur $i$ , dans le cadre des jeux pondérés, peut être mesuré par le nombre de fois où il est décisif, pondéré par son poids $w i$ .
La fraction de pouvoir absolu total qu'un joueur possède définit donc son pouvoir.
Remarque: La justification donné par l'auteur est principalement d'ordre théorique vu qu'il s'agit pour lui de proposer une sophistication de l'indice normalisé de Banzhaf $B i (v)$ dotée de "bonnes" propriétés, que ne possède pas l'indice d'origine.
L'indice de Chakravarty du joueur $i$ dans le jeu $v :[q; w 1,..., w n]$ est donné par:

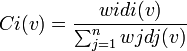
$Ci(v) = \frac {widi(v)} {\sum_{j=1}^n wjdj(v)}$

En reprenant l'exemple n°2, on obtient:

$Ca(v) = \frac{2}{3}$
$Ci(v) = \frac{1}{9} , \forall i = b,c,d$

Éléments de comparaison

Interprétation probabiliste des indices de pouvoirs

Découverte: ces substances courantes accélèrent le vieillissement

Il y a 16 heures

Des scientifiques identifient le meilleur moment de la journée pour faire du sport

Il y a 16 heures

Cette rupture technologique pourrait décupler la capacité des disques durs

Il y a 21 heures

Cycle menstruel: une étude scientifique établit un lien avec la Lune

Il y a 21 heures

Quand un trio d'étoiles devient un couple: une histoire cataclysmique retracée

Il y a 23 heures

Ce petit ver possède des yeux immenses: pourquoi ?

Il y a 23 heures

D'où vient cette structure fractale observée dans une bactérie ?

Il y a 1 jour

Découverte majeure dans les allergies respiratoires

Il y a 1 jour

Voici ce qui a produit la lumière la plus lumineuse jamais détectée dans l'Univers

Il y a 1 jour

Propagation inquiétante de la "mouche noire" suceuse de sang en Allemagne

Il y a 1 jour

Le hasard confère le prix Turing et 1 million de dollars au mathématicien Avi Wigderson

Il y a 1 jour

AI Act: comment encadrer l'intelligence artificielle en Europe ?

Il y a 1 jour

Quelle est cette forme étrange photographiée près de la Lune ?

Il y a 2 jours

Si vous avez déjà eu une entorse de la cheville, attention à ceci

Il y a 2 jours

Démonstration d'une nouvelle technologie de lévitation, stable et sans supraconductivité

Il y a 2 jours

Ces indices d'une rupture imminente de la faille de San Andreas

Il y a 2 jours

Cet effet inattendu de la musculation sur la mémoire

Il y a 2 jours

Les géantes Uranus et Neptune ne seraient pas faites comme nous l'imaginions

Il y a 2 jours

Parker Solar Probe se prépare à battre le record de vitesse de l'humanité

Il y a 3 jours

Nos ancêtres à l'époque des dinosaures

Il y a 3 jours

Observer directement le Big Bang avec un télescope plus puissant que le James Webb ?

Il y a 3 jours

Découverte de 17 variants génétiques liés à la maladie d'Alzheimer

Il y a 3 jours

Un immense glacier du Groenland est littéralement en train de fondre sous nos yeux

Il y a 3 jours

Découverte: des bactéries anticholestérol dans notre intestin

Il y a 3 jours

Des dinosaures aux oiseaux: cette anomalie de l'ADN a trompé les scientifiques

Il y a 4 jours

De la vie cachée 800 mètres sous terre: comment est-ce possible ?

Il y a 4 jours

Analyse d'un signal radio inhabituel, en provenance de cet objet spatial extrême

Il y a 4 jours

Ce liquide est programmable, pouvant changer de consistance et de couleur

Il y a 4 jours

Un trou noir trop léger, ou une étoile à neutrons trop lourde ? L'objet qui intrigue les scientifiques

Il y a 4 jours

Un lien démontré entre vapotage, petit-déjeuner et maux de tête

Il y a 4 jours

Un immense "arc-en-ciel" détecté sur une exoplanète

Il y a 5 jours

Des scientifiques étudient 40 ans de vie marine dans... des conserves de saumon

Il y a 5 jours

Cette innovation va améliorer significativement la sensibilité des détecteurs d'ondes gravitationnelles

Il y a 5 jours

Découverte d'une ingénierie humaine vieille de... 300 000 ans

Il y a 5 jours

Psyche: une mission à la découverte de ce très mystérieux objet spatial

Il y a 6 jours

Peur généralisée: des scientifiques découvrent comment ne pas être tétanisé par la peur

Il y a 6 jours

Découverte accidentelle d'une mémoire quantique au potentiel énorme

Il y a 6 jours

Des chercheurs ont créé artificiellement des "minifoies"

Il y a 6 jours

Surprise: la surface lunaire a "coulé" sous la croûte

Il y a 7 jours

Un curieux "point de bascule" découvert dans l'évolution des champignons

Il y a 7 jours

Des humains préhistoriques ont gravé ces traces de dinosaures

Il y a 7 jours

Ralentissement significatif d'importants courants océaniques: des répercussions graves ?

Il y a 7 jours

Les étoiles à neutrons, des aspirateurs de matière noire ?

Il y a 7 jours

Greffer de la peau de porc pour soigner les plaies

Il y a 7 jours

Le secret d'une jeunesse éternelle à proximité du trou noir de notre Voie Lactée

Il y a 8 jours

Une quantité phénoménale de volcans cachés sous l'Antarctique: des risques d'éruption ?

Il y a 8 jours

Une mission spatiale dans l'espace interstellaire, à 1000 unités astronomiques ?

Il y a 8 jours

Ce régime montre une efficacité contre la maladie d'Alzheimer

Il y a 8 jours

Les dinosaures contredisent ce principe scientifique

Il y a 8 jours

Sentons-nous le goût des aliments uniquement avec notre langue ?

Il y a 8 jours

Populaires

Voici ce qui a produit la lumière la plus lumineuse jamais détectée dans l'Univers

Parker Solar Probe se prépare à battre le record de vitesse de l'humanité

De la vie cachée 800 mètres sous terre: comment est-ce possible ?

Ces indices d'une rupture imminente de la faille de San Andreas

Découverte: ces substances courantes accélèrent le vieillissement

Cette rupture technologique pourrait décupler la capacité des disques durs

Toutes les ventes flash et Codes Promos Amazon

Cdiscount: les meilleures réductions actuelles

Page générée en 2.066 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise