Théorie des jeux - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La théorie des jeux constitue une approche mathématique de problèmes de stratégie tels qu’on en trouve en recherche opérationnelle et en économie. Elle étudie les situations où les choix de deux protagonistes - ou davantage - ont des conséquences pour l’un comme pour l’autre. Le jeu peut être à somme nulle (ce qui est gagné par l’un est perdu par l’autre, et réciproquement) ou, plus souvent, à somme non-nulle. Un exemple de jeu à somme nulle est celui de la mourre, ou celui du pierre-feuille-ciseaux.
Historique
Trois grandes étapes
- La théorie des jeux initiale, de John von Neumann et Oskar Morgenstern, utilisait des cas de choix qui restaient les mêmes au cours du temps, et qui étaient à somme nulle.
- Les jeux à somme non-nulle furent étudiés ensuite, et utilisés dans la théorie de la négociation. On découvrit que leur étude permettait d’aborder de façon mathématique des questions jusque là restées d’ordre philosophique, comme la morale.
- On s’intéressa ensuite aux jeux où le choix se posait en termes différents à chaque étape, que l’on nomma un temps théorie des jeux combinatoires. Celle-ci est plutôt aujourd’hui, pour des raisons de commodité et de communauté de concepts, considérée comme une branche soit de la théorie des graphes, soit de ce qu’on nomme l’intelligence artificielle.
Détails
La théorie des jeux a fait l’objet de résultats assez anciens, à partir des travaux de Blaise Pascal sur le "problème des partis", donnant une première intuition des probabilités et de l’espérance mathématique, et de son étonnant pari. Elle n'est devenue une branche importante des mathématiques qu’à partir des années 1940. Surtout après la publication de la Théorie des jeux et du comportement économique (Theory of Games and Economic Behavior) par John von Neumann et Oskar Morgenstern, en 1944. Cet ouvrage fondateur détaillait la méthode de résolution des jeux à somme nulle.
Lors de sa présentation, la théorie rencontra une vive opposition de la part des états-majors. Ceux-ci acceptaient volontiers l’usage de tirages au hasard dans les jeux de Kriegspiel des écoles militaires. Mais l’idée de remettre au sort, le fait d’escorter réellement ou non tel ou tel convoi, au nom des stratégies mixtes, ne les enthousiasmait guère. Issus du terrain et sachant ce qu’étaient des pertes humaines, ils jugeaient le procédé, pour le moins, cavalier.
Vers 1950, John Nash a présenté une définition d’une stratégie optimale, pour un jeu à plusieurs joueurs, dite équilibre de Nash. Ce résultat tardif génial a été raffiné par Reinhard Selten ; cela leur a valu le « prix Nobel d'économie » en 1994, pour leurs travaux sur la théorie des jeux, avec John Harsanyi qui avait travaillé sur les jeux en information incomplète.
L’association entre jeu et nombres surréels de Conway a été établie dans les années 1970.
Types de jeux
La théorie des jeux classifie les jeux en catégories en fonction de leurs approches de résolution. Les catégories les plus ordinaires sont :
Jeux coopératifs et compétitions
Les jeux coopératifs sont des jeux dans lesquels on cherche la meilleure situation pour les joueurs sur des critères tels que la justice, l'entraide. On considère qu'ensuite les joueurs vont jouer ce qui aura été choisi, il s'agit d'une approche normative. Par exemple, à un croisement, chacun des deux automobilistes a la possibilité de passer ou non. Le code de la route impose sa stratégie à chacun des joueurs par une signalisation.
Dans les jeux coopératifs, on étudie la formation de coalitions entre les joueurs afin d’obtenir un meilleur résultat pour ses membres. C’est un concept qui n’existe pas dans les jeux non coopératifs. Le jeu non coopératif à n joueurs est une simple généralisation du jeu à deux joueurs. Par contre, dans un jeu coopératif à deux personnes, il n’y a qu’une seule coalition, et même avec quatre joueurs, il n'y aura qu'une seule coopération puisque le principe du jeu coopératif est que les joueurs s'associent pour lutter contre le jeu lui-même. Sinon, on parlera peut-être de jeu semi-coopératif coopétitif, où les joueurs peuvent former des coopérations temporaires contre les autres. Un autre concept utilisé dans les jeux coopératifs est la fonction caractéristique. Soit v(C) la fonction qui donne la valeur maximin de la coalition C. Cette expression est appelée la fonction caractéristique du jeu. Par exemple, si la coalition comprenant les joueurs 1 et 2 obtient un profit de 600, on écrit v(1,2) = 600.
On peut décrire un jeu en indiquant les valeurs de la fonction caractéristique pour toutes les coalitions possibles, y compris celles ne comprenant qu'un seul joueur. On parle souvent du jeu v au lieu de dire un jeu ayant la fonction caractéristique v.
Dans un jeu à n personnes, il y a 2n − 1 coalitions non vides et autant de valeurs de la fonction caractéristique. Par définition, la valeur de la fonction caractéristique d'une coalition vide est égale à zéro.
Si des coalitions disjointes (C et Z) sont réunies en une grande coalition, on peut admettre que la valeur de la fonction caractéristique de cette grande coalition soit au moins égale à la somme des valeurs des deux coalitions:
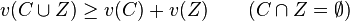
(propriété de superadditivité)
Soit N={1,2,…,n} l’ensemble des joueurs et xi la somme ou l’utilité que le joueur i reçoit. Une imputation est un vecteur
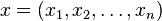

L’ensemble des imputations qui ne sont pas dominées est appelé le noyau ou le coeur d’un jeu coopératif. L’imputation du noyau ne peut pas être bloquée par aucune autre imputation.
Par exemple, le jeu avec les fonctions caractéristiques suivantes:
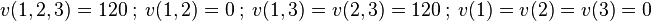
a un noyau correspondant au point (0,0,120). Il suffit de modifier une fonction caractéristique (par exemple, v(1,2)=120) pour obtenir un noyau vide.
Plusieurs autres solutions d’un jeu coopératif ont été proposées, entre autres la valeur de Shapley qui est une imputation unique.
Théorie de la négociation
La théorie moderne de la négociation est articulée sur le fait qu’une négociation constitue un jeu à somme non-nulle. L’art de la négociation consiste donc moins à faire céder l’interlocuteur sur la ligne principale d’opposition (un prix, par exemple) qu’à trouver des arrangements extérieurs à cette ligne qui apporteront beaucoup à l’un sans coûter trop cher à l’autre (stratégies dites Gagnant-gagnant).
Depuis longtemps, tout cela était utilisé dans les négociations :
- « Je ne peux accepter ce coût FOB, mais puis le considérer en CIF. »
- « Si je vous en prends deux, m’accordez-vous 5% de remise ? »
- « Je vous en offre tant, mais il faut vous décider tout de suite. »
voire entre particuliers :
- « Je veux bien te le laisser à ce prix-là, mais tu offres le café ! »
« Coopétition »
La coopétition est le partage d'information au sein d'un réseau socio-professionnel de concurrence. On parle aussi de compétition transparente. La coopétition peut s'appliquer tant à des services de recherche et développement des organisations (qui se livrent par ailleurs une guerre féroce en matière commerciale), qu'au monde du développement des logiciels libres, qui fait appel au principes de fourches (un projet se scinde en deux en cas de passage de la coopération à la compétition), tout en laissant les deux codes logiciels produits en concurrence accessibles pour les deux groupes de développeurs. Par extension, la coopétition s'applique dans tout contexte de gestion de la complexité socio-professionnelle, car le principe de base est que l'information prend de la valeur lorsqu'elle est partagée, et que justement, c'est en étant émetteur d'information stratégiques qu'on prend une position dominante dans un groupe de compétiteurs, face à divers clients potentiels.
Jeux de stratégie à somme nulle et non nulle
- Les jeux à somme nulle sont tous les jeux où la somme « algébrique » des gains des joueurs est nulle. Ce que gagne l’un est nécessairement perdu par un autre, l'enjeu est la répartition du total fixé, qu'on peut supposer réparti à l'avance, ce qui ramène au cas où les gains sont vraiment nuls (d'où la dénomination). Les échecs ou le poker sont des jeux à somme nulle car les gains de l’un sont très exactement les pertes de l’autre.
- Les situations d’affaires, la vie politique ou le dilemme du prisonnier sont des jeux à somme non-nulle car certaines issues sont globalement plus profitables pour tous, ou plus dommageables pour tous. On a commencé historiquement par étudier les jeux à somme nulle, plus simples. Au-delà de la matière-énergie avec la loi de la conservation de la somme algébrique nulle, le jeu à somme non-nulle est concevable, dans lequel le gain de l'un peut profiter à l'autre. Tel est le cas avec l'information, la communication et l'apprentissage où l'information est une des trois composantes fondamentales avec la matière et l'énergie. L'exemple illustratif le plus simple est l'information génétique de l'ADN transcrite sur l'ARN pour être « lue », « traduite » et organiser la matière et l'énergie biologiques. En sciences sociales, on cite parfois l'idéologie d'harmonie industrielle du Japon moderne (coalition tripartite capital-travail-gouvernement) comme exemple de jeu à somme non nulle. Dans le commerce international, l'exemple de ce jeu à somme non nulle est la concurrence coopérative des Tigres asiatiques et Dragons asiatiques où le gain de l'un profite aux autres, dans la foulée du miracle économique japonais des années 1950-1960 qui a ouvert les portes à la Corée, à Hong Kong, à Singapour, à Taïwan et au Viêt Nam, dans une coévolution technico-commerciale.
- En écologie, la coévolution est un autre exemple, dans la nature, de la somme non nulle où le changement de l'un facilite et fait la promotion du changement de l'autre.
On pourrait croire qu'il suffirait pour ramener un jeu à somme non-nulle à un jeu à somme nulle d'y ajouter un joueur simplet, le « tableau », sorte de non-player character qui compenserait les pertes nettes des joueurs. Ce n’est pas le cas : un joueur est censé défendre rationnellement ses intérêts dans la mesure de ses possibilités; cet ajout formel, introduisant une dissymétrie entre les « vrais » joueurs et le « tableau », complique l'analyse et celle-ci y perd plus qu’elle n’y gagne.
Jeu synchrone ou asynchrone
Dans un jeu synchrone, les joueurs décident de leur coup simultanément, sans savoir ce que les autres jouent. Dans un jeu asynchrone (ou alternatif, à deux joueurs), ils jouent les uns après les autres, en disposant à chaque fois de l’information sur le coup de l’adversaire. Une analyse des stratégies gagnantes est proposée pour le hex, un jeu de cette nature.
Jeux répétés
La répétition d’un jeu, avec connaissance des résultats intermédiaires, change souvent fondamentalement son déroulement (les meilleurs coups et la conclusion).
Par exemple, il peut être utile de prendre ponctuellement le risque de perdre « pour voir », tester les autres joueurs, et mettre en place des stratégies de communication par les coups joués (à défaut d’autre moyen de communication).
Il se développe également des phénomènes de réputation qui vont influencer les choix stratégiques des autres joueurs. Dans le dilemme du prisonnier, le fait de savoir qu’on va jouer plusieurs fois avec un dur qui n’avoue jamais mais se venge cruellement, ou avec un lâche qui avoue toujours, change radicalement la stratégie optimale.
Enfin, curieusement, le fait que le nombre total de parties soit connu à l’avance ou non peut avoir des effet importants sur le résultat, l’ignorance du nombre de coups rapprochant du jeu avec un nombre infini de coup, alors que sa connaissance rapproche au contraire du jeu à un seul coup (et ce, aussi grand que soit le nombre de coups !)
Information complète, information parfaite
On dit qu'un jeu est à information complète si chaque joueur connaît lors de la prise de décision :
- ses possibilités d'action
- les possibilités d'action des autres joueurs
- les gains résultants de ces actions
- les motivations des autres joueurs
Par ailleurs on parle de jeu à information parfaite dans le cas de jeu à mécanisme séquentiel, où chaque joueur a connaissance en détail de toutes les actions effectuées avant son choix.
Les échecs sont à information complète et parfaite. Du fait de l'incertitude sur les gains (cartes de l'adversaire cachées), le poker est à information incomplète. La phase d'enchères vérifie les propriétés d'information parfaite, mais en assimilant le tirage des cartes à l'action d'un joueur fictif (souvent appelé Nature), la théorie des jeux exclut en général le poker des jeux à information parfaite.
Les situations réelles sont rarement en information complète, et ce cas ne sert souvent qu’aux approximations confiantes.
Les jeux en information incomplète sont des situations stratégiques où l'une des conditions n'est pas vérifiée. Ce peut être par l'intervention du hasard au cours du jeu (cas fréquent dans les jeux de société), ou parce qu'une des motivations d'un acteur est cachée (domaine important pour l'application de la théorie des jeux à l'économie).
Les jeux en information à la fois imparfaite et incomplète sont de loin les plus complexes. Dans ces jeux certains joueurs peuvent disposer d'informations propres sur la manière dont le hasard va intervenir dans l'issue du jeu (une meilleure connaissance des probabilités d'occurrence de tel ou tel événement qui va affecter le cours du jeu, par exemple). Les jeux de guerre (war games) relèvent typiquement de cette catégorie, l'aléa sur la réussite d'un engagement entre corps de troupes dépendant d'informations non partagées par les adversaires sur les rapports de force entre ces troupes.
Pour être complet, il convient aussi de distinguer les jeux à mémoire parfaite et à mémoire imparfaite. Les jeux à mémoire « parfaite » sont des situations où chaque joueur peut se rappeler à tout moment de la suite de coups qui ont été joués précédemment, au besoin en notant au fur et à mesure les coups joués. Les jeux à mémoire « imparfaite » supposent une sorte d'amnésie de la part des joueurs. Les jeux de guerre sont des exemples de jeux à mémoire imparfaite si les commandements de zones opérationnelles ne parviennent pas à communiquer entre eux ou avec l'État-Major et donc n'ont pas trace des mouvements déjà effectués par les troupes amies lorsqu'elles doivent décider de leurs propres mouvements. Un jeu typique est le 21 ou blackjack : la convention selon laquelle la suite de paquets de cartes n’est pas battue entre deux jeux peut donner un léger avantage au joueur dès lors que celui-ci prend en compte cette information partielle.
Jeux déterminés
Les jeux de Nim forment un cas particulier de jeu à somme nulle, sans intervention du hasard et dans la plupart des cas à nombre de situations finies. Dans leur cas particulier, la théorie des graphes fournit un outil plus utile que la théorie des jeux à proprement parler. La notion de noyau du jeu (ensemble des nœuds depuis lesquels la victoire est assurée si l’on y parvient en cours de jeu et qu’on joue de façon optimale ensuite) y est caractérisée.