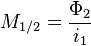Inductance - Définition
La liste des auteurs de cet article est disponible ici.
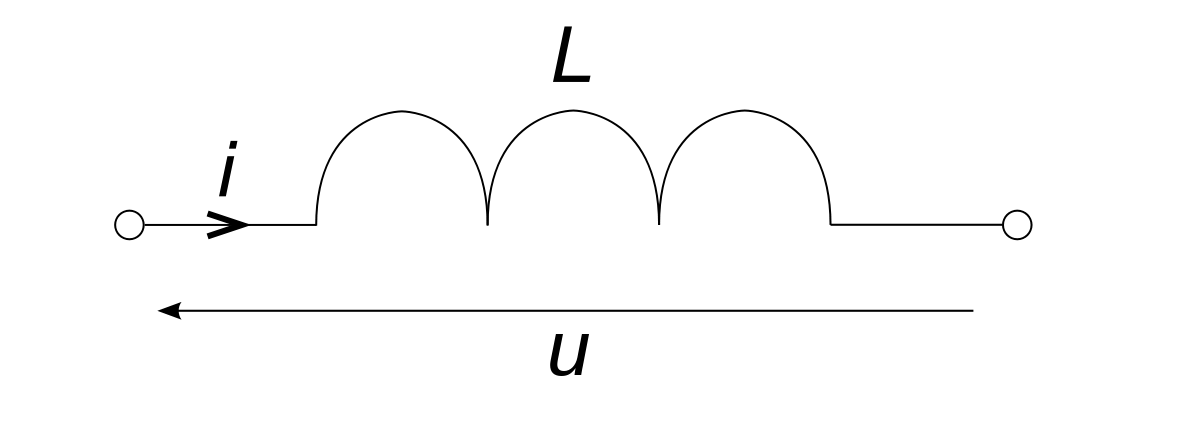
Le dipôle « Inductance », ou bobine
Son symbole dans les schémas est L. Une bobine d'inductance L est un dipôle tel que la tension à ces bornes soit proportionnelle à la dérivée de l'intensité du courant qui le traverse en convention récepteur :
Cette relation vient de l’expression du flux du champ magnétique et de la loi de Faraday qui seront vues en magnétostatique :
-
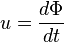
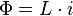
Cette équation montre que l’intensité du courant traversant une inductance ne peut pas subir de discontinuité, cela correspondrait en effet à une tension infinie à ses bornes, donc à une puissance infinie.
Puissance instantanée
Remarque : on ne peut stocker que de l'énergie. Le terme puissance emmagasinée est donc un abus de langage qui correspond en réalité à la puissance que l'on fournit à l'inductance et qui vient augmenter l'énergie emmagasinée dans cette dernière.
En convention récepteur la puissance instantanée fournie à l'inductance est égale à :
En utilisant la transformation mathématique suivante :
on obtient la relation :
La puissance instantanée fournie à une inductance est liée à la variation du carré de l’intensité qui la traverse : si celui-ci augmente, l’inductance emmagasine de l'énergie. Elle en restitue dans le cas contraire.
L’énergie échangée entre 2 instants ti et tf vaut :
Il en résulte qu’il est difficile de faire varier rapidement le courant qui circule dans une bobine et ceci d’autant plus que la valeur de son inductance sera grande. Cette propriété est souvent utilisée pour supprimer de petites variations de courant non désirées.
L’effet de l’inductance face aux variations du courant est analogue en mécanique à l’effet de la masse face aux variations de la vitesse : quand on veut augmenter la vitesse il faut fournir de l’énergie cinétique et ceci d’autant plus que la masse est grande. Quand on veut freiner, il faut récupérer cette énergie. Débrancher une bobine parcourue par un courant, c’est un peu arrêter une voiture en l’envoyant contre un mur.
Puissance en régime sinusoïdal
En régime sinusoïdal, une inductance idéale (dont la résistance est nulle) ne consomme pas de puissance active. En revanche, il y a stockage ou restitution d’énergie par la bobine lors des variations de l'intensité du courant.
Impédance
À chaque instant
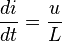
On a
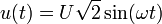
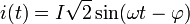
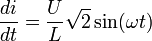
Donc
On obtient finalement :
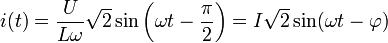
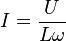
- Loi d'Ohm en valeurs efficaces :
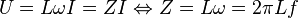
- En continu, f = 0: une bobine parfaite se comporte comme un court-circuit (en effet :
![Z = 0 \Rightarrow U = 0\cdot I = 0[V]](https://static.techno-science.net/illustration/Definitions/autres/1/1703b94d5ded1d9b72d60462edccfe63_671f10062988425a469b14789604cf88.png)
En complexes
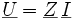
D'où :
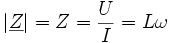
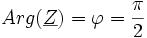
On en déduit que
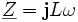
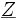
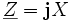
Inductance mutuelle
Lorsqu’un circuit 1 traversé par un courant noté
La valeur de cette inductance mutuelle dépend des deux circuits en présence (caractéristiques géométriques, nombre de spires) mais aussi de leur position relative : éloignement et orientation.
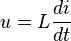
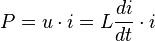
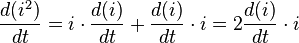
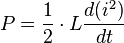
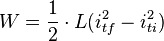

![\underline{U} = [U, 0]](https://static.techno-science.net/illustration/Definitions/autres/a/a022edbfa88f01df2752797598dd9f90_0c5a352f0680b892cf4ea7abf207d8b2.png)
![\underline{I} = [I = \frac{U}{L\omega}, -\frac{\pi}{2} rad]](https://static.techno-science.net/illustration/Definitions/autres/d/d09820292aa0405a8fa69b05eb6141e2_ff5ebeded5e6091343444b5c91c60ed5.png)