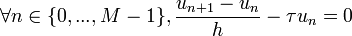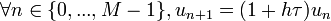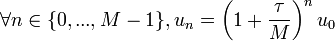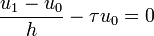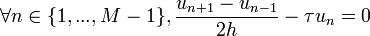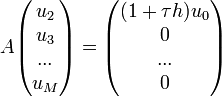Méthode des différences finies - Définition

Schéma numérique

Écrire un schéma numérique de résolution de l'équation différentielle initiale signifie :

• substituer les formulations des dérivées/différentielles obtenues par approximation aux opérateurs eux-mêmes sur tous les points du maillage.

• réorganiser les équations pour faire apparaître un schéma explicite (ex : les valeurs à la date t+1 données en fonction des valeurs des dates 0 à t) ou implicite (une équation lie les valeurs passées, présentes et futures sans qu'on arrive à exprimer ces dernières seules).

Dans un cadre de modélisation classique d'opérateurs linéaires dans des équations différentielles linéaires, on aboutit à un système d'équations linéaires de dimension égale au nombre de nœuds du maillage (en fait un peu moins, du fait des données initiales, par exemple).

Résoudre le schéma numérique signifie simplement trouver les valeurs discrètes de la fonction en chaque nœud.

Un système issu d'une équation linéaire peut souvent être algébriquement simple à résoudre. Pour simplifier, on peut dire que les schémas explicites engendrent des systèmes d'équation à matrice triangulaire ou trigonalisables, ce qui n'est pas le cas des schémas implicites.

Les méthodes de résolution des schémas peuvent faire appel à des méthodes d'optimisation comme à des méthodes algébriques classiques.

Exemple de schéma numérique

Partons de l'équation suivante :

Alors, on choisit d'écrire le schéma d'ordre 1 de la dérivée première en tous les points d'un maillage à pas constant {x₀ = 0,x₁ = h,x₂ = 2h,...,x_M = Mh = 1}. On recherche exactement M inconnues, les valeurs qu'on écrira . Le schéma est alors appelé schéma d'Euler explicite d'ordre 1 :

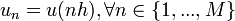
Ce qui donne explicitement la relation de récurrence entre u_n et son successeur u_{n + 1}

Soit une suite géométrique qui nous donne assez facilement, en remplaçant h par sa valeur :

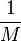
On dispose donc pour tous les points du maillage de la valeur de la solution du problème selon la méthode des différences finies. Pour les points non contenus sur le maillage, il faudra alors faire une hypothèse sur la qualité de la solution, par exemple supposer que la fonction est constante ou affine par morceaux.

Choisissons plutôt de partir du schéma d'ordre 2 de la dérivée première, sauf pour le point n = 1 pour lequel on reprend le schéma d'ordre 1 :

Ceci nous donne alors

où la matrice A est tridiagonale, avec des − 2τh sur la diagonale, des 1 sur la 1ère surdiagonale et des -1 sur la 1ère sousdiagonale.