Méthode des différences finies - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Dans le domaine de l'analyse numérique, on peut être amené à rechercher la solution d'une équation aux dérivées partielles. Parmi les méthodes de résolutions couramment pratiquées, la méthode des différences finies est la plus facile d'accès, puisqu'elle repose sur deux notions : la discrétisation des opérateurs de dérivation/différentiation (assez intuitive) par différences finies d'une part, et la convergence du schéma numérique ainsi obtenu d'autre part.
Approximation des opérateurs par formules de Taylor
Grâce aux formules de Taylor, on définit la discrétisation des opérateurs différentiels (dérivées premières, secondes, etc, partielles ou non).
La formulation de Taylor-Young est préférable dans son utilisation simple, la formulation de Taylor avec reste intégral de Laplace permet de mesurer les erreurs (cf. plus bas)
Exemple d'approximation d'opérateur
Par exemple, écrivons en un point x et pour une valeur h telle que u est dérivable trois fois sur un intervalle contenant strictement [x − h,x + h], on sait écrire les deux formules de Taylor-Young :
et :
où toutes les applications
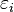
et en sommant les développements pour x-h et x+h l'on obtient:
on obtient respectivement des approximations de 1er ordre et 2nd ordre en h.
Degré de dérivation
Pour des raisons à la fois d'écriture algébrique et d'étude de convergence/stabilité a priori il est important de se replacer autant que possible dans une problématique avec des ordres de dérivation les plus faibles possible, quitte à augmenter la dimension de l'espace d'étude. On fera ainsi appel à des variables intermédiaires : les dérivées ou dérivées partielles des fonctions initialement étudiées.
Exemple d'abaissement de degré de dérivation
- u''(x) + ω2u(x) = 0,u(0) = u0,u'(0) = u1
s'écrira volontiers avec le choix :
ce qui donnera l'équation pour U :
Avec
Donc le degré de dérivation est ici réduit à 1, alors que la dimension de l'espace d'arrivée est devenue 2.
Maillage
Un maillage est un ensemble de points du domaine de définition sur lequel on va appliquer la méthode des différences finies. Pour une application définie sur un segment de

On appelle le pas du maillage la distance entre deux points successifs du maillage voisins. En dimension 1, cela se simplifie en différence des abscisses. Ce pas n'est pas nécessairement constant, il peut même être judicieux de ne pas le fixer comme tel. Le pas (global) de l'approximation peut être défini comme le plus grand pas du maillage. Ainsi, si ce pas global tend vers 0, cela veut dire que la répartition des points du maillage dans l'intervalle choisi tend à se faire sur tout le domaine d'étude par densité.
Exemple de maillage
Pour un intervalle de validité [0,1] on utilisera (M + 1) points, par exemple {0,h,2h,...,Mh = 1} pour un pas constant
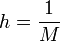
Convergences
La deuxième notion complète la première. Elle traite de la convergence d'un schéma numérique. En effet, une modélisation par différences finies est un couple (conditions (initiales, finales, etc), schéma numérique) dont on ne sait a priori pas si son éventuelle solution est proche ou non d'une solution réelle espérée du système initial (conditions (initiales, finales, etc), équations différentielles). Pour parler de convergence, il est nécessaire de comprendre celle-là selon un critère similaire à ceux-ci, si on étudie une fonction f sur un intervalle [a,b] :
- convergence simple : en n'importe quel point l'approximation évaluée tend vers la vraie valeur de la solution quand le pas tend vers 0
- convergence en norme 2
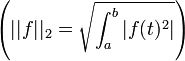
- convergence absolue ou en norme absolue
![\left( ||f||_\infty = \max_{ t \in [a,b] }{|f(t)|} \right)](https://static.techno-science.net/illustration/Definitions/autres/0/0c39ec6226ec0a8041a3a00e25f51d89_d37665ce787c922182cad9e277692d87.png)
On doit alors étudier la qualité de la convergence de ce schéma numérique selon des critères tels que la stabilité, la robustesse et bien-sûr différentes normes (2 ou
- La stabilité, la robustesse du schéma : [à rajouter]
Exemple d'erreur d'approximation
Pour un maillage donné, l'erreur entre la solution approchée et la solution réelle est déterminée par l'erreur de troncature, comme définie notamment dans le théorème de Taylor avec reste intégral ou au sens de la restriction à une partie finie d'une série de Taylor qui possède un nombre infini de termes.
Là encore, l'erreur dépend de ce qu'on entend mesurer. L'erreur peut en effet être mesurée point par point (convergence simple) ou selon une norme 2 ou infinie.
Dans le dernier exemple présenté, on connaît la solution exacte de l'équation, qui est une fonction exponentielle.
- u(x) = u0e(τx)
On sait donc évaluer la différence directement entre la version réelle et la version estimée par approximation pour un maillage M intervalles :
Ici, on a une mesure exacte de l'erreur point par point. Notons qu'on peut aussi démontrer que si le maillage s'affine infiniment (c'est-à-dire que le nombre de points M tend vers l'infini), alors la convergence simple est assurée. Prenons un exemple : le point

Si M est pair, alors le point
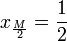
Or, un résultat classique d'analyse nous donne la limite de la suite
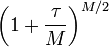
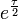
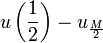
Il est en fait possible, en utilisant le caractère archimédien et la continuité des solutions, de montrer que la convergence simple est assurée partout...
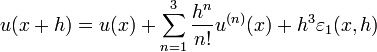
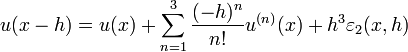
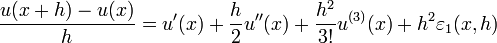
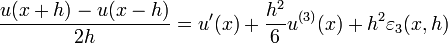
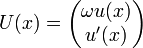
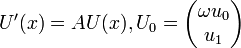
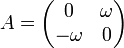
![\forall n \in \{ 0, ..., M \}, u( x_n ) - u_n = u_0 \left[ e^{ \frac{ \tau n }{M}} - \left( 1 + \frac{ \tau }{ M } \right)^n \right]](https://static.techno-science.net/illustration/Definitions/autres/3/37f65c3d1c1b4e0838528cdfd2159924_2f1ce3a55a3aefba58306f46310a0fb3.png)
![u\left( \frac{1}{2} \right) - u_{ \frac{M}{2} }= u_0 \left[ e^{ \frac{ \tau }{2}} - \left( 1 + \frac{ \tau }{ M } \right)^{ M / 2 } \right]](https://static.techno-science.net/illustration/Definitions/autres/e/e8aa13087f1e8440f2a8cdf36152f5c1_6a61f867150e4c5bf60415c318865c5e.png)

















































