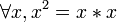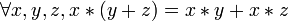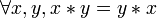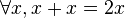Méthode formelle (informatique) - Définition

Introduction

En informatique, les méthodes formelles sont des techniques permettant de raisonner rigoureusement, à l'aide de logique mathématique, sur des programmes informatiques ou des matériels électroniques, afin de démontrer leur validité par rapport à une certaine spécification.

Ces méthodes permettent d'obtenir une très forte assurance de l'absence de bug dans les logiciels, c'est-à-dire d'acquérir des niveaux d'évaluation d'assurance élevés, elles sont basées sur les sémantiques des programmes, c'est-à-dire sur des descriptions mathématiques formelles du sens d'un programme donné par son code source (ou parfois, son code objet). Cependant, elles sont généralement coûteuses en ressources (humaines et matérielles) et actuellement réservées aux logiciels les plus critiques. Leur amélioration et l'élargissement de leurs champs d'application pratique sont la motivation de nombreuses recherches scientifiques en informatique.

Exemple

Comment vérifier que l' identité (a + b)² = a² + b² + 2(a * b) est correcte ?

Une vérification naïve pourrait consister à examiner toutes les valeurs possibles de a, à les croiser avec toutes les valeurs possibles de b et, pour chaque couple, à calculer (a + b)², puis a² + b² + 2(a * b) et à s'assurer que l'on obtient le même résultat. Si les domaines de a et de b sont grands, cette vérification peut être très longue. Et si les domaines sont infinis (par exemple les réels), cette vérification ne peut pas être exhaustive.

En vérification formelle, on utilise des valeurs symboliques et on applique les règles qui régissent le + et l' * . Ici, les règles pourraient être:

En se servant de ces règles, on arrive à montrer que (a + b)² = a² + b² + 2(a * b).

Catégories

Différents corpus mathématiques ont été utilisés pour élaborer des raisonnements formels sur les logiciels. Cette diversité d'approche a engendré des «familles» de méthodes formelles. Citons notamment («Les méthodes basées sur ...» ):

• Le model checking analyse exhaustivement l'évolution du système lors de ses exécutions possibles. Par exemple, pour démontrer l'absence d'erreurs à l'exécution, on pourra tester l'absence d'états d'erreur dans l'ensemble des états accessibles du système. Il s'agit alors d'une forme de test (informatique) exhaustif, mais mené à l'aide d'algorithmes astucieux permettant d'énumérer les états du système sous une forme symbolique économique. En général, il n'est pas possible d'analyser directement le système, mais on en analyse plutôt un modèle informatique, plus ou moins abstrait par rapport à la réalité (voir aussi interprétation abstraite). Dans les évolutions récentes du software model-checking, l'analyseur peut automatiquement enrichir le modèle pour en obtenir un moins abstrait; des preuves peuvent être fournies après des itérations de ce processus, qui peut ne pas converger.

• L'analyse statique par interprétation abstraite, schématiquement, calcule symboliquement un sur-ensemble des états accessibles du système.

• La preuve automatique de théorème tend à démontrer automatiquement des théorèmes sur les formules logiques décrivant la sémantique du programme.

• Les assistants de preuve permettent à l'utilisateur de démontrer des théorèmes sur le programme, avec une aide (plus ou moins grande) et une vérification par la machine.

Il existe des gradations et des mélanges possibles entre ces méthodes. Par exemple, un assistant de preuve pourra être suffisamment automatisé pour prouver automatiquement la plupart des lemmes utilitaires d'une preuve de programmes. Un model-checker pourra être appliqué sur un modèle construit à l'aide d'un prouveur automatique de théorèmes. Une interprétation abstraite préalable pourra limiter le nombre de cas à démontrer dans une preuve de théorèmes, etc.

Les méthodes formelles peuvent s'appliquer à différent stade du processus de développement d'un système (logiciel, électronique, mixte), de la spécification jusqu'à la réalisation finale. Voir l'exemple de la méthode B.