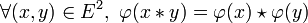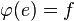Monoïde - Définition

Définition

Formellement, est un monoïde lorsque :

1. (stabilité)
2. (associativité)
3. (élément neutre)

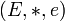
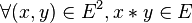
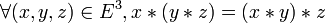
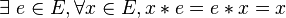
Un monoïde E est dit simplifiable à gauche, ou encore régulier à gauche, (resp. à droite) si

(resp. ) .

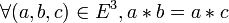
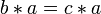
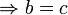
On dit que deux éléments x, y d'un monoïde commutent (l'un avec l'autre) ou sont permutables (l'un avec l'autre) si :

x * y = y * x.

Un monoïde est dit commutatif si sa loi de composition est commutative, c'est-à-dire si :

,

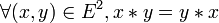
ce qui revient à dire que tous les éléments de E commutent l'un avec l'autre.

Bases et monoïdes libres

Une partie P d'un monoïde (E, * ,e) est appelée base de E si c'est une famille génératrice de E dans laquelle tout élément se décompose de façon unique. C'est-à-dire si

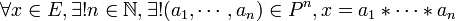
Un monoïde est dit libre s'il admet une base. Dans ce cas, la base est unique.

• e n'appartient jamais à la base, sans quoi les éléments auraient une infinité de décomposition possible.

• Si A est un ensemble (appelé parfois alphabet), l'ensemble des suites finies d'éléments de A (appelées mots) muni de l'opération de concaténation est un monoïde libre noté A ^* et appelé monoïde libre sur A. Sa base est l'ensemble des mots de longueur un, et donc assimilable naturellement à l'alphabet.

• Deux monoïdes libres sur des alphabets finis sont si et seulement si leurs bases ont même cardinal.

• Dans un monoïde libre l'élément neutre est le seul élément .

Sous-monoïde

Un sous-monoïde d'un monoïde est un sous ensemble de vérifiant:

1. (stable)
2. 

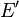
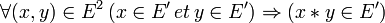
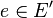
Famille génératrice de sous-monoïde

Soit P une partie d'un monoïde (E, * ,e). On appelle sous-monoïde engendré par P (noté P ^* ) le plus petit sous-monoïde de E contenant P. Il peut être défini par :

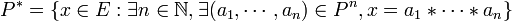
P est appelé est famille génératrice de P ^* .

• Notons que l'élément e fait bien toujours partie de P ^*  : il admet une décomposition constituée par un produit vide (n = 0).

• On peut toujours trouver une famille génératrice à tout monoïde, la plus triviale étant lui-même.

Morphisme de monoïde

• Soit et deux monoïdes. on appelle morphisme de vers toute application de E vers F telle que

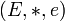
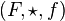
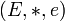
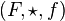
La première propriété est celle de morphisme de loi ou morphisme de magma.

• La composée de deux morphismes de monoïde est un morphisme de monoïde.
• La réciproque de tout morphisme bijectif de monoïde est un morphisme de monoïde. En conséquence, un morphisme bijectif est qualifié d'isomorphisme.
• L'image d'un élément idempotent par un morphisme de monoïde est un élément idempotent.
• Si on munit l'ensemble des entiers naturels de la loi Max, l'application est un morphisme de loi mais n'est pas un morphisme de monoïde.
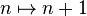
• Tout morphisme de loi d'un monoïde vers un groupe est un morphisme de monoïde.
• L'image d'un sous-monoïde par un morphisme de monoïde est un sous-monoïde. En particulier l'image d'un morphisme de monoïde est un sous-monoïde.

• On appelle noyau d'un morphisme de monoïde l'ensemble des antécédents de l'élément neutre.

Attention, il n'y a pas de lien clair entre noyau et injectivité lorsque le monoïde n'est pas un groupe. Par exemple, l'application est un endomorphisme du monoïde des entiers naturels muni de la loi Max.

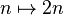
• L'image réciproque d'un sous-monoïde par un sous-monoïde est un sous-monoïde. En particulier le noyau d'un morphisme de monoïde est un sous-monoïde.