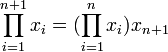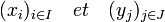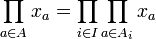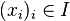Monoïde - Définition

Introduction

En mathématiques, un monoïde est une structure algébrique consistant en un ensemble muni d'une loi de composition interne associative et d'un élément neutre. Un monoïde est donc un magma associatif, c.à.d. un demigroupe, et unifère.

Préambule

Il arrive parfois qu'une structure composée d'un ensemble et d'une unique opération soit relativement pauvre en propriétés élémentaires, par exemple un anneau où l'on considère uniquement la multiplication. Une telle structure est appelée monoïde. La pauvreté en question rend difficile l'établissement de théorèmes nombreux ou puissants. Pour pallier cette faiblesse, une technique consiste à enrichir le monoïde pour en faire un groupe. Cette méthode est utilisée en théorie algébrique des nombres dans le cas des idéaux de la fermeture intégrale d'un corps de nombre, on travaille alors essentiellement sur le groupe des classes d'idéaux.

Parfois, cette technique ne correspond pas au besoin. Tel est le cas pour l'étude des polynômes en plusieurs indéterminées. On construit l'algèbre sur un monoïde particulier, engendré par un ensemble d'indices.

Composé d'une séquence (finie) d'éléments

Soit E un monoïde. Notons sa loi de composition sous forme multiplicative, c'est-à-dire que nous écrirons xy pour désigner le composé noté plus haut. L'élément neutre est alors désigné par 1.
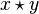
Nous nous proposons de définir le composé (« produit » dans notre notation) d'un n-uplet d'éléments de E, quel que soit le nombre naturel .
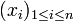
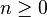
Étant donné un tel n-uplet, nous pouvons construire par récurrence sur i un (n+1)-uplet d'éléments de E en posant :

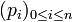
p₀ = 1

et

.

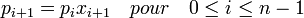
Nous définissons alors le composé du n-uplet comme étant p_n. On note ce composé

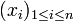
ou encore

.

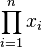
On montre facilement par récurrence sur i que si est un (n+1)-uplet d'éléments de E, les n+1 « produits partiels » p_i associés comme ci-dessus au n-uplet (plus petit) sont les n+1 premiers des n+2 produits partiels associés au (n+1)-uplet , d'où la formule

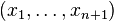
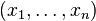
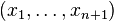
qu'on peut encore écrire

.

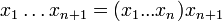
Cette formule, ou la formule

,

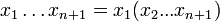
est couramment présentée comme définition de par récurrence sur n. Du fait de l'associativité, ces deux formules fournissent la même définition. En effet, avec la définition que nous avons choisie, on prouve par récurrence sur s que, pour tous nombres naturels r et s, pour tout r-uplet et tout s-uplet d'éléments de E,

,

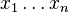
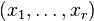
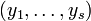
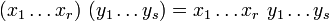
ce qui permet de prouver l'équivalence des deux définitions par récurrence sur le nombre de facteurs.

D'après ces définitions, le produit de la famille vide (ou 0-uplet) est égal à 1.

On appelle séquence d'éléments de E une famille d'éléments de E indexée par un ensemble fini totalement ordonné. On associe de façon évidente à une telle séquence un n-uplet d'éléments de E, ce qui permet d'étendre de façon évidente la définition du composé d'un n-uplet d'éléments de E à toute séquence d'éléments de E. Deux séquences

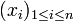
sont dites équivalentes s'il existe un isomorphisme σ d'ensembles ordonnés de I sur J tel que, pour tout élément i de I,

y_σ(i) = x_i.

Cela équivaut à ce que les n-uplets correspondant à ces deux séquences soient identiques, donc deux séquences équivalentes ont le même composé.

La considération des séquences permet de formuler comme suit le théorème d'associativité :

Soit E un monoïde, noté multiplicativement, soit A un ensemble fini totalement ordonné, soit une famille finie de parties deux à deux disjointes de A dont la réunion est A tout entier. (On n'exclut pas que certains des ensembles considérés soient vides.) On suppose que si i et j sont deux éléments de I tels que i < j, alors a < b pour tout élément a de A_i et tout élément b de A_j. Pour toute séquence d'éléments de E indexée par A, on a

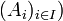
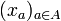
Si le monoïde E est commutatif, on peut définir le composé d'une famille finie d'éléments de E sans préciser un ordre sur l'index de cette famille, car on prouve que le composé, tel que défini ci-dessus, est alors indépendant de l'ordre choisi. Plus généralement, si E est un monoïde non forcément commutatif, si

est une famille d'éléments de E dont tous les éléments commutent l'un avec l'autre, le produit des éléments de cette famille ne dépend pas de l'ordre choisi. C'est le « théorème de commutativité ».