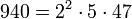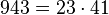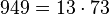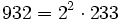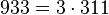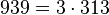Nombres 900 à 999 - Définition

Entiers de 940 à 949

---

Pour l'année, voir 940

• 

---

Pour l'année, voir 941

• un nombre premier,
• la somme de trois nombres premiers consécutifs (311 + 313 + 317),
• la somme de cinq nombres premiers consécutifs (179 + 181 + 191 + 193 + 197),
• un nombre premier de Chen,
• un nombre premier d’Eisenstein sans partie imaginaire

---

Pour l'année, voir 942

• ,
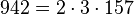
• un nombre sphénique,
• la somme de quatre nombres premiers consécutifs (229 + 233 + 239 + 241),
• un anti-indicateur

---

Pour l'année, voir 943

• 

---

Pour l'année, voir 944

• ,
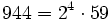
• un anti-indicateur

---

Pour l'année, voir 945

• ,
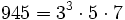
• la double factorielle de 9,
• un nombre abondant (la somme des diviseurs moins lui-même est de 975)
• un nombre de Leyland

---

Pour l'année, voir 946

• ,
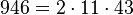
• un nombre sphénique,
• un nombre triangulaire,
• un nombre hexagonal

---

Pour l'année, voir 947

• un nombre premier,
• la somme de sept nombres premiers consécutifs (113 + 127 + 131 + 137 + 139 + 149 + 151),
• un nombre premier de Chen,
• un nombre premier balancé,
• un nombre premier d’Eisenstein sans partie imaginaire

---

Pour l'année, voir 948

• ,
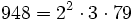
• un anti-indicateur

---

Pour l'année, voir 949

• 

Entiers de 930 à 939

---

Pour l'année, voir 930

• ,
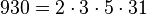
• un nombre oblong

---

Pour l'année, voir 931

• ,
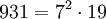
• la somme de trois nombres premiers consécutifs (307 + 311 + 313)

---

Pour l'année, voir 932

• 

---

Pour l'année, voir 933

• 

---

Pour l'année, voir 934

• ,
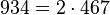
• un anti-indicateur

---

Pour l'année, voir 935

• ,
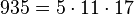
• un nombre sphénique,
• un nombre Harshad

---

Pour l'année, voir 936

• ,
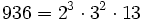
• un nombre pentagonal pyramidal,
• un nombre Harshad

---

Pour l'année, voir 937

• un nombre premier,
• un nombre premier de Chen,
• un nombre étoilé

---

Pour l'année, voir 938

• ,
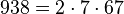
• un nombre sphénique,
• un anti-indicateur

---

Pour l'année, voir 939

• 

Entiers de 960 à 969

---

Pour l'année, voir 960

• ,
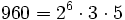
• la somme de six nombres premiers consécutifs (149 + 151 + 157 + 163 + 167 + 173),
• un nombre Harshad,
• un identifiant du groupe ISBN pour les livres publiés en Grèce

---

Pour l'année, voir 961

• 961 = 31²,
• la somme de trois nombres premiers consécutifs (313 + 317 + 331),
• la somme de cinq nombres premiers consécutifs (181 + 191 + 193 + 197 + 199),
• un nombre octogonal centré,
• un identifiant du groupe ISBN pour les livres publiés en Slovénie

---

Pour l'année, voir 962

• ,
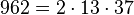
• un nombre sphénique,
• un anti-indicateur,
• un des deux identifiants du groupe ISBN pour les livres publiés à Hong Kong

---

Pour l'année, voir 963

• ,
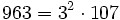
• la somme des vingt-quatre premiers nombres premiers ,
• un identifiant du groupe ISBN pour les livres publiés en Hongrie

---

Pour l'année, voir 964

• ,
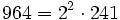
• la somme de quatre nombres premiers consécutifs (233 + 239 + 241 + 251),
• un anti-indicateur,
• un identifiant du groupe ISBN pour les livres publiés en Iran

---

Pour l'année, voir 965

• ,
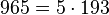
• un identifiant du groupe ISBN pour les livres publiés en Israël

---

Pour l'année, voir 966

• ,
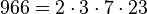
• la somme de huit nombres premiers consécutifs (103 + 107 + 109 + 113 + 127 + 131 + 137 + 139),
• un nombre Harshad,
• un des deux identifiants du groupe ISBN pour les livres publiés en Ukraine

---

Pour l'année, voir 967

• un nombre premier,
• un des deux identifiants du groupe ISBN pour les livres publiés en Malaisie

---

Pour l'année, voir 968

• ,
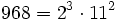
• un anti-indicateur,
• un des deux identifiants du groupe ISBN pour les livres publiés au Mexique

---

Pour l'année, voir 969

• ,
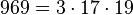
• un nombre sphénique,
• un nombre ennéagonal,
• un nombre tétraédrique,
• un identifiant du groupe ISBN pour les livres publiés au Pakistan