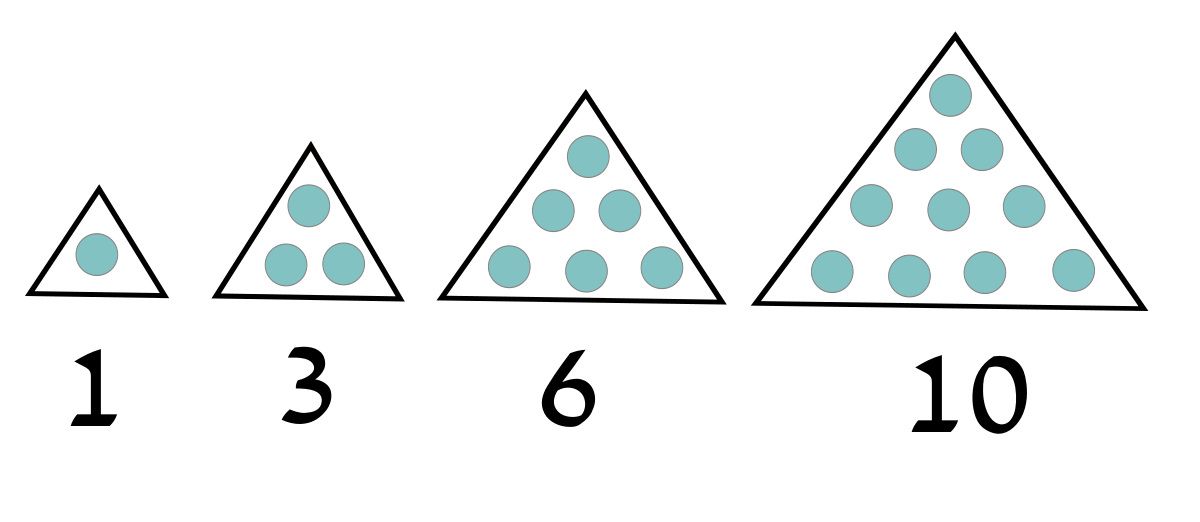Nombre triangulaire - Définition

Introduction

En arithmétique, un nombre triangulaire est un cas particulier de nombre figuré. Il correspond à un nombre entier positif égal au nombre de pastilles dans un triangle construit à la manière de la figure de droite. Cette figure montre que 28 est le septième nombre triangulaire, ou encore le nombre triangulaire d'indice 7. Une définition plus formelle s'obtient par récurrence : le nombre triangulaire d'indice 1 est égal à 1, et un nombre triangulaire est égal à son prédécesseur additionné de son indice. Les premiers nombres triangulaires sont : 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 ... Il existe différentes manières de calculer le nombre triangulaire d'indice n, l'une d'elle est graphique et s'obtient par un raisonnement d'arithmétique géométrique. On trouve, si t_n désigne le nombre triangulaire d'indice n : :

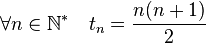
Cette formule est ancienne, on la doit à l'école de Pythagore et est probablement connue depuis le début du V^e siècle avant Jésus Christ.

Définition et calculs

Définitions

La représentation figurée permet un calcul pour les premières valeurs.

Formellement, un nombre triangulaire se définit comme une suite, notée (t_n) dans cet article, où n est un indice parcourant les nombres entiers strictement positifs :

Une autre manière de définir cette suite est une récurrence. Les deux formulations sont équivalentes :

Définition — Le nombre triangulaire d'indice 1 est 1, le nombre triangulaire d'indice n est défini par la formule suivante :

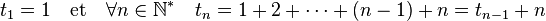
Chez les pythagoriciens, le quatrième nombre triangulaire, c'est à dire 10 est nommé tetraktys. Il dispose d'une dimension symbolique.

Remarque :

Méthodes de calcul

Une représentation permet le calcul d'un nombre triangulaire.

Une vielle méthode de calcul provient de l'école pythagoricienne. Les grecs de cette époque usaient de géométrie pour résoudre les questions de cette nature. Cette approche est qualifiée d'arithmétique géométrique. La figure de droite permet de comprendre comment ils calculaient le nombre triangulaire d'indice 8. La zone rouge de la figure correspond au nombre triangulaire d'indice 8, c'est à dire la somme 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8. A cette zone rouge, on accole la zone bleue de la figure, contenant exactement le même nombre de pastilles que la rouge. Cette zone contient un nombre de pastilles égal à deux fois le nombre triangulaire d'indice 8, ou encore 8 x 9 pastilles. Ce résultat est obtenu en remarquant que la zone bleu et rouge est un rectangle de base 9 et de hauteur 8. Le double du nombre triangulaire d'indice 8 est égal à 8 x 9 = 72, ce nombre est égal à 36. On retrouve bien la formule annoncée en introduction.

Une légende infondée prête à Carl Friedrich Gauss l'exploit suivant. Alors que Gauss avait huit ans, son maître d'école Büttner demanda aux élèves de sa classe d'additionner tous les nombres de 1 à 100. Gauss additionne 1 avec 100, puis 2 avec 99, puis 3 avec 98 et ainsi de suite jusqu'à 50 avec 51. Il obtient une somme de 50 fois la valeur 101, soit 5 050. Seule l'anecdote est infondée, la méthode, en revanche est pertinente.

Une autre méthode consiste à utiliser une récurrence pour montrer la formule de sommation de l'introduction. A l'ordre 0, la formule est manifestement exacte. On la suppose vraie à l'ordre n - 1 :

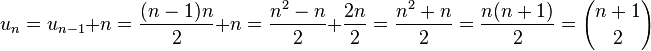
Le dernier terme est l'expression du nombre triangulaire d'indice n sous la forme d'un coefficient binomiale. Il correspond au nombre de paires distinctes contenues dans un ensemble à n + 1 éléments.