Polynôme minimal trigonométrique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Polynôme minimaux de nombres de la forme 2cos(kπ/n) ou 2sin(kπ/n). - Formules générales en relation avec les coefficients des polynomes minimaux trigonométriques. - Polynômes minimaux de nombres de la forme tan(kπ/n).

Formules générales en relation avec les coefficients des polynomes minimaux trigonométriques.

On trouvera ci-dessous quelques formules relatives aux relations entre coefficients et racines d'un polynome annulateur des nombres trigonométriques traités dans cet article. Certaines de ces formules font apparaître au second membre la racine d'un diviseur du dénominateur se trouvant dans l'argument des fonctions trigonométriques au premier membre. Ce qui permet d'entrevoir les raisons pour lesquelles, on trouve dans les coefficients du polynôme minimal de telle racines.

Formules de sommations

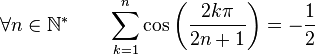
$\forall n \in \mathbb{N}^* \qquad \sum_{k=1}^n \cos\left(\frac{2k\pi}{2n+1}\right) = -\frac{1}{2} ~$

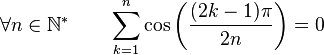
$\forall n \in \mathbb{N}^* \qquad \sum_{k=1}^n \cos\left(\frac{(2k-1)\pi}{2n}\right) = 0 ~$

Formules de produits

(Dans ce qui suit Ent(x) désigne la partie entière de x)

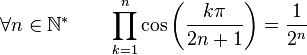
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^n \cos\left(\frac{k\pi}{2n+1}\right) = \frac{1}{2^n} ~$

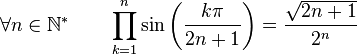
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^n \sin\left(\frac{k\pi}{2n+1}\right) = \frac{\sqrt{2n+1}}{2^n} ~$

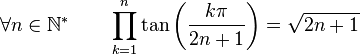
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^n \tan\left(\frac{k\pi}{2n+1}\right) = \sqrt{2n+1} ~$

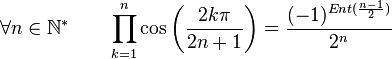
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^n \cos\left(\frac{2k\pi}{2n+1}\right) = \frac{(-1)^{Ent(\frac{n-1}{2})}}{2^n} ~$

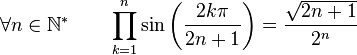
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^n \sin\left(\frac{2k\pi}{2n+1}\right) = \frac{\sqrt{2n+1}}{2^n} ~$

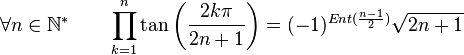
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^n \tan\left(\frac{2k\pi}{2n+1}\right) = (-1)^{Ent(\frac{n-1}{2})}\sqrt{2n+1} ~$

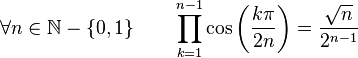
$\forall n \in \mathbb{N}-\left\{0,1\right\} \qquad \prod_{k=1}^{n-1} \cos\left(\frac{k\pi}{2n}\right) = \frac{\sqrt{n}}{2^{n-1}} ~$

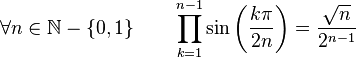
$\forall n \in \mathbb{N}-\left\{0,1\right\} \qquad \prod_{k=1}^{n-1} \sin\left(\frac{k\pi}{2n}\right) = \frac{\sqrt{n}}{2^{n-1}} ~$

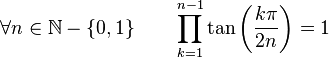
$\forall n \in \mathbb{N}-\left\{0,1\right\} \qquad \prod_{k=1}^{n-1} \tan\left(\frac{k\pi}{2n}\right) = 1 ~$

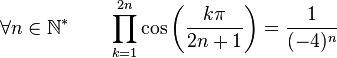
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^{2n} \cos\left(\frac{k\pi}{2n+1}\right) = \frac{1}{(-4)^n} ~$

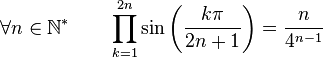
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^{2n} \sin\left(\frac{k\pi}{2n+1}\right) = \frac{n}{4^{n-1}} ~$

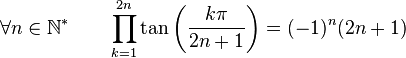
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^{2n} \tan\left(\frac{k\pi}{2n+1}\right) = (-1)^n(2n+1) ~$

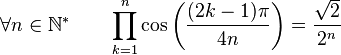
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^{n} \cos\left(\frac{(2k-1)\pi}{4n}\right) = \frac{\sqrt{2}}{2^n} ~$

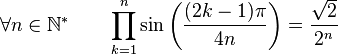
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^{n} \sin\left(\frac{(2k-1)\pi}{4n}\right) = \frac{\sqrt{2}}{2^n} ~$

$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^{n} \tan\left(\frac{(2k-1)\pi}{4n}\right) = 1 ~$

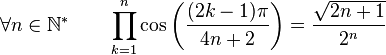
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^{n} \cos\left(\frac{(2k-1)\pi}{4n+2}\right) = \frac{\sqrt{2n+1}}{2^n} ~$

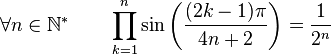
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^{n} \sin\left(\frac{(2k-1)\pi}{4n+2}\right) = \frac{1}{2^n} ~$

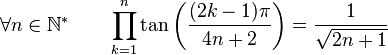
$\forall n \in \mathbb{N}^* \qquad \prod_{k=1}^{n} \tan\left(\frac{(2k-1)\pi}{4n+2}\right) = \frac{1}{\sqrt{2n+1}} ~$

Dans la suite, on désignera par P(n), l'ensemble des nombres entiers inférieurs à n et premier avec n. Par exemple :

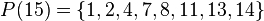
$P(15) = \left\{ 1,2,4,7,8,11,13,14 \right\}$

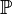
On désignera aussi par $\mathbb{P}$ , l'ensemble des nombres premiers.

On a alors :

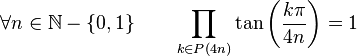
$\forall n \in \mathbb{N}-\left\{0,1\right\} \qquad \prod_{k \in P(4n)} \tan\left(\frac{k\pi}{4n}\right) = 1 ~$

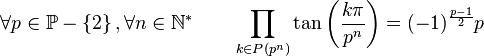
$\forall p \in \mathbb{P}-\left\{2\right\}, \forall n \in \mathbb{N}^* \qquad \prod_{k \in P(p^n)} \tan\left(\frac{k\pi}{p^n}\right) = (-1)^\frac{p-1}{2}p ~$

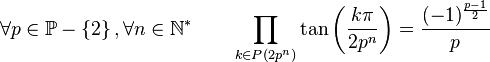
$\forall p \in \mathbb{P}-\left\{2\right\}, \forall n \in \mathbb{N}^* \qquad \prod_{k \in P(2p^n)} \tan\left(\frac{k\pi}{2p^n}\right) = \frac{(-1)^\frac{p-1}{2}}{p} ~$

Pour tout n ayant au moins 2 nombres premiers impairs dans sa décomposition en facteurs premiers, on a :

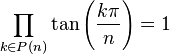
$\prod_{k \in P(n)} \tan\left(\frac{k\pi}{n}\right) = 1 ~$

Pour tout n qui n'est pas une puissance de 2, on a :

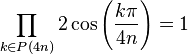
$\prod_{k \in P(4n)} 2\cos\left(\frac{k\pi}{4n}\right) = 1 ~$

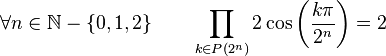
$\forall n \in \mathbb{N}-\left\{0,1,2\right\} \qquad \prod_{k \in P(2^n)} 2\cos\left(\frac{k\pi}{2^n}\right) = 2 ~$

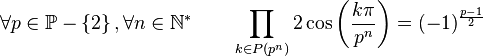
$\forall p \in \mathbb{P}-\left\{2\right\}, \forall n \in \mathbb{N}^* \qquad \prod_{k \in P(p^n)} 2\cos\left(\frac{k\pi}{p^n}\right) = (-1)^\frac{p-1}{2} ~$

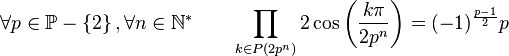
$\forall p \in \mathbb{P}-\left\{2\right\}, \forall n \in \mathbb{N}^* \qquad \prod_{k \in P(2p^n)} 2\cos\left(\frac{k\pi}{2p^n}\right) = (-1)^\frac{p-1}{2}p ~$

Pour tout n ayant au moins 2 nombres premiers impairs dans sa décomposition en facteurs premiers, on a :

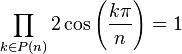
$\prod_{k \in P(n)} 2\cos\left(\frac{k\pi}{n}\right) = 1 ~$

Si 2n+1 est une puissance d'un nombre premier p,

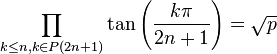
$\prod_{k \le n, k \in P(2n+1)} \tan\left(\frac{k\pi}{2n+1}\right) = \sqrt{p} ~$

Si 2n+1 contient au moins deux nombres premiers distincts dans sa décomposition en facteurs premiers,

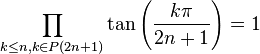
$\prod_{k \le n, k \in P(2n+1)} \tan\left(\frac{k\pi}{2n+1}\right) = 1 ~$

Etc...

Polynômes minimaux de nombres de la forme tan(kπ/n).

Ci-dessous se trouvent, dans l'ordre des degrés croissants, les premiers polynômes minimaux des nombres de la forme tan(kπ/n).

Polynômes du premier degré

$x - 1 \qquad x + 1$

sont respectivement les polynômes minimaux des nombres :

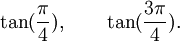
$\tan(\frac{\pi}{4}), \qquad \tan(\frac{3\pi}{4}). ~$

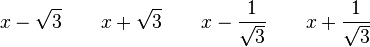
$x - \sqrt{3} \qquad x + \sqrt{3} \qquad x - \frac{1}{\sqrt{3}} \qquad x + \frac{1}{\sqrt{3}}$

sont respectivement les polynômes minimaux dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

$\tan(\frac{\pi}{3}), \qquad \tan(\frac{2\pi}{3}), \qquad \tan(\frac{\pi}{6}), \qquad \tan(\frac{5\pi}{6}). ~$

Polynômes du second degré

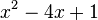
$x^2 - 4x + 1 ~$

Est le polynôme minimal des nombres :

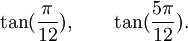
$\tan(\frac{\pi}{12}), \qquad \tan(\frac{5\pi}{12}). ~$

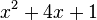
$x^2 + 4x + 1 ~$

Est le polynôme minimal des nombres :

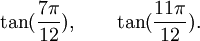
$\tan(\frac{7\pi}{12}), \qquad \tan(\frac{11\pi}{12}). ~$

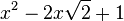
$x^2 - 2x\sqrt{2} + 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{2})[X]$ des nombres :

$\tan(\frac{\pi}{8}), \qquad \tan(\frac{3\pi}{8}). ~$

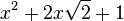
$x^2 + 2x\sqrt{2} + 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{2})[X]$ des nombres :

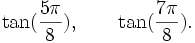
$\tan(\frac{5\pi}{8}), \qquad \tan(\frac{7\pi}{8}). ~$

Polynômes du troisième degré

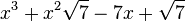
$x^3 + x^2\sqrt{7} - 7x + \sqrt{7} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{7})[X]$ des nombres :

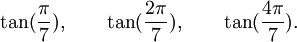
$\tan(\frac{\pi}{7}), \qquad \tan(\frac{2\pi}{7}), \qquad \tan(\frac{4\pi}{7}). ~$

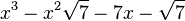
$x^3 - x^2\sqrt{7} - 7x - \sqrt{7} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{7})[X]$ des nombres :

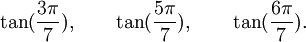
$\tan(\frac{3\pi}{7}), \qquad \tan(\frac{5\pi}{7}), \qquad \tan(\frac{6\pi}{7}). ~$

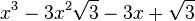
$x^3 - 3x^2\sqrt{3} - 3x + \sqrt{3} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

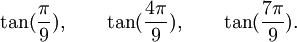
$\tan(\frac{\pi}{9}), \qquad \tan(\frac{4\pi}{9}), \qquad \tan(\frac{7\pi}{9}). ~$

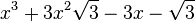
$x^3 + 3x^2\sqrt{3} - 3x - \sqrt{3} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

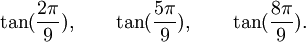
$\tan(\frac{2\pi}{9}), \qquad \tan(\frac{5\pi}{9}), \qquad \tan(\frac{8\pi}{9}). ~$

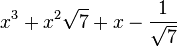
$x^3 + x^2\sqrt{7} + x - \frac{1}{\sqrt{7}} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{7})[X]$ des nombres :

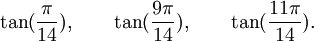
$\tan(\frac{\pi}{14}), \qquad \tan(\frac{9\pi}{14}), \qquad \tan(\frac{11\pi}{14}). ~$

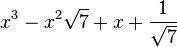
$x^3 - x^2\sqrt{7} + x + \frac{1}{\sqrt{7}} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{7})[X]$ des nombres :

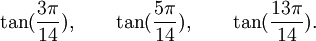
$\tan(\frac{3\pi}{14}), \qquad \tan(\frac{5\pi}{14}), \qquad \tan(\frac{13\pi}{14}). ~$

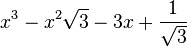
$x^3 - x^2\sqrt{3} - 3x + \frac{1}{\sqrt{3}} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

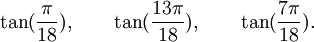
$\tan(\frac{\pi}{18}), \qquad \tan(\frac{13\pi}{18}), \qquad \tan(\frac{7\pi}{18}). ~$

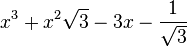
$x^3 + x^2\sqrt{3} - 3x - \frac{1}{\sqrt{3}} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

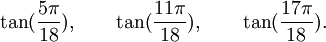
$\tan(\frac{5\pi}{18}), \qquad \tan(\frac{11\pi}{18}), \qquad \tan(\frac{17\pi}{18}). ~$

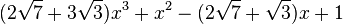
$(2\sqrt{7} + 3\sqrt{3})x^3 + x^2 - (2\sqrt{7} + \sqrt{3})x + 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})(\sqrt{7})[X]$ des nombres :

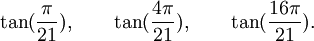
$\tan(\frac{\pi}{21}), \qquad \tan(\frac{4\pi}{21}), \qquad \tan(\frac{16\pi}{21}). ~$

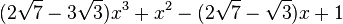
$(2\sqrt{7} - 3\sqrt{3})x^3 + x^2 - (2\sqrt{7} - \sqrt{3})x + 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})(\sqrt{7})[X]$ des nombres :

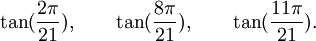
$\tan(\frac{2\pi}{21}), \qquad \tan(\frac{8\pi}{21}), \qquad \tan(\frac{11\pi}{21}). ~$

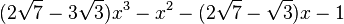
$(2\sqrt{7} - 3\sqrt{3})x^3 - x^2 - (2\sqrt{7} - \sqrt{3})x - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})(\sqrt{7})[X]$ des nombres :

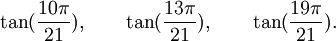
$\tan(\frac{10\pi}{21}), \qquad \tan(\frac{13\pi}{21}), \qquad \tan(\frac{19\pi}{21}). ~$

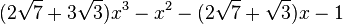
$(2\sqrt{7} + 3\sqrt{3})x^3 - x^2 - (2\sqrt{7} + \sqrt{3})x - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})(\sqrt{7})[X]$ des nombres :

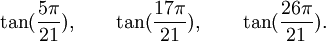
$\tan(\frac{5\pi}{21}), \qquad \tan(\frac{17\pi}{21}), \qquad \tan(\frac{26\pi}{21}). ~$

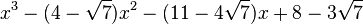
$x^3 - (4 - \sqrt{7})x^2 - (11 - 4\sqrt{7})x + 8 - 3\sqrt{7} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{7})[X]$ des nombres :

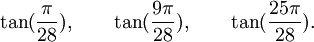
$\tan(\frac{\pi}{28}), \qquad \tan(\frac{9\pi}{28}), \qquad \tan(\frac{25\pi}{28}). ~$

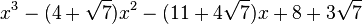
$x^3 - (4 + \sqrt{7})x^2 - (11 + 4\sqrt{7})x + 8 + 3\sqrt{7} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{7})[X]$ des nombres :

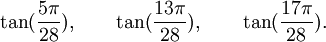
$\tan(\frac{5\pi}{28}), \qquad \tan(\frac{13\pi}{28}), \qquad \tan(\frac{17\pi}{28}). ~$

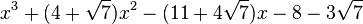
$x^3 + (4 + \sqrt{7})x^2 - (11 + 4\sqrt{7})x - 8 - 3\sqrt{7} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{7})[X]$ des nombres :

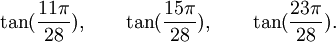
$\tan(\frac{11\pi}{28}), \qquad \tan(\frac{15\pi}{28}), \qquad \tan(\frac{23\pi}{28}). ~$

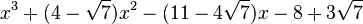
$x^3 + (4 - \sqrt{7})x^2 - (11 - 4\sqrt{7})x - 8 + 3\sqrt{7} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{7})[X]$ des nombres :

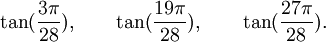
$\tan(\frac{3\pi}{28}), \qquad \tan(\frac{19\pi}{28}), \qquad \tan(\frac{27\pi}{28}). ~$

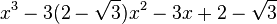
$x^3 - 3(2 - \sqrt{3})x^2 - 3x + 2 - \sqrt{3} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

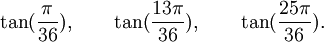
$\tan(\frac{\pi}{36}), \qquad \tan(\frac{13\pi}{36}), \qquad \tan(\frac{25\pi}{36}). ~$

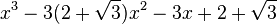
$x^3 - 3(2 + \sqrt{3})x^2 - 3x + 2 + \sqrt{3} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

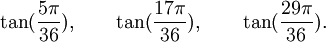
$\tan(\frac{5\pi}{36}), \qquad \tan(\frac{17\pi}{36}), \qquad \tan(\frac{29\pi}{36}). ~$

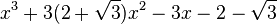
$x^3 + 3(2 + \sqrt{3})x^2 - 3x - 2 - \sqrt{3} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

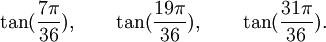
$\tan(\frac{7\pi}{36}), \qquad \tan(\frac{19\pi}{36}), \qquad \tan(\frac{31\pi}{36}). ~$

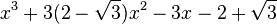
$x^3 + 3(2 - \sqrt{3})x^2 - 3x - 2 + \sqrt{3} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

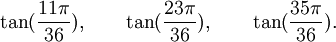
$\tan(\frac{11\pi}{36}), \qquad \tan(\frac{23\pi}{36}), \qquad \tan(\frac{35\pi}{36}). ~$

Polynômes du quatrième degré

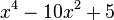
$x^4 - 10x^2 + 5 ~$

Est le polynôme minimal des nombres :

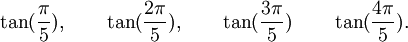
$\tan(\frac{\pi}{5}), \qquad \tan(\frac{2\pi}{5}), \qquad \tan(\frac{3\pi}{5}) \qquad \tan(\frac{4\pi}{5}) . ~$

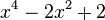
$x^4 - 2x^2 + 2 ~$

Est le polynôme minimal des nombres :

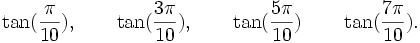
$\tan(\frac{\pi}{10}), \qquad \tan(\frac{3\pi}{10}), \qquad \tan(\frac{5\pi}{10}) \qquad \tan(\frac{7\pi}{10}) . ~$

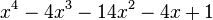
$x^4 - 4x^3 - 14x^2 - 4x + 1 ~$

Est le polynôme minimal des nombres :

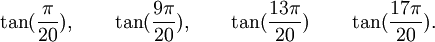
$\tan(\frac{\pi}{20}), \qquad \tan(\frac{9\pi}{20}), \qquad \tan(\frac{13\pi}{20}) \qquad \tan(\frac{17\pi}{20}) . ~$

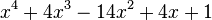
$x^4 + 4x^3 - 14x^2 + 4x + 1 ~$

Est le polynôme minimal des nombres :

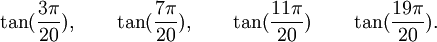
$\tan(\frac{3\pi}{20}), \qquad \tan(\frac{7\pi}{20}), \qquad \tan(\frac{11\pi}{20}) \qquad \tan(\frac{19\pi}{20}) . ~$

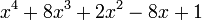
$x^4 + 8x^3 + 2x^2 - 8x + 1 ~$

Est le polynôme minimal des nombres :

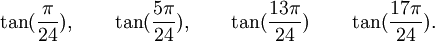
$\tan(\frac{\pi}{24}), \qquad \tan(\frac{5\pi}{24}), \qquad \tan(\frac{13\pi}{24}) \qquad \tan(\frac{17\pi}{24}) . ~$

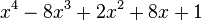
$x^4 - 8x^3 + 2x^2 + 8x + 1 ~$

Est le polynôme minimal des nombres :

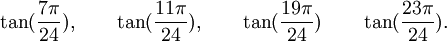
$\tan(\frac{7\pi}{24}), \qquad \tan(\frac{11\pi}{24}), \qquad \tan(\frac{19\pi}{24}) \qquad \tan(\frac{23\pi}{24}) . ~$

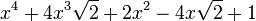
$x^4 + 4x^3\sqrt{2} + 2x^2 - 4x\sqrt{2}+ 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{2})[X]$ des nombres :

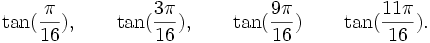
$\tan(\frac{\pi}{16}), \qquad \tan(\frac{3\pi}{16}), \qquad \tan(\frac{9\pi}{16}) \qquad \tan(\frac{11\pi}{16}) . ~$

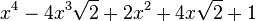
$x^4 - 4x^3\sqrt{2} + 2x^2 + 4x\sqrt{2}+ 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{2})[X]$ des nombres :

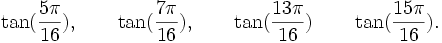
$\tan(\frac{5\pi}{16}), \qquad \tan(\frac{7\pi}{16}), \qquad \tan(\frac{13\pi}{16}) \qquad \tan(\frac{15\pi}{16}) . ~$

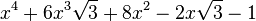
$x^4 + 6x^3\sqrt{3} + 8x^2 - 2x\sqrt{3} - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

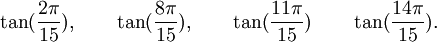
$\tan(\frac{2\pi}{15}), \qquad \tan(\frac{8\pi}{15}), \qquad \tan(\frac{11\pi}{15}) \qquad \tan(\frac{14\pi}{15}) . ~$

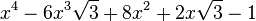
$x^4 - 6x^3\sqrt{3} + 8x^2 + 2x\sqrt{3} - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

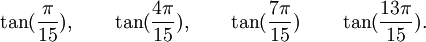
$\tan(\frac{\pi}{15}), \qquad \tan(\frac{4\pi}{15}), \qquad \tan(\frac{7\pi}{15}) \qquad \tan(\frac{13\pi}{15}) . ~$

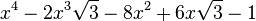
$x^4 - 2x^3\sqrt{3} - 8x^2 + 6x\sqrt{3} - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

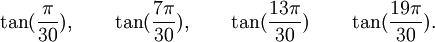
$\tan(\frac{\pi}{30}), \qquad \tan(\frac{7\pi}{30}), \qquad \tan(\frac{13\pi}{30}) \qquad \tan(\frac{19\pi}{30}) . ~$

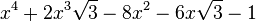
$x^4 + 2x^3\sqrt{3} - 8x^2 - 6x\sqrt{3} - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

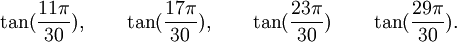
$\tan(\frac{11\pi}{30}), \qquad \tan(\frac{17\pi}{30}), \qquad \tan(\frac{23\pi}{30}) \qquad \tan(\frac{29\pi}{30}) . ~$

Polynômes du cinquième degré

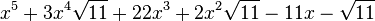
$x^5 + 3x^4\sqrt{11} + 22x^3 + 2x^2\sqrt{11} - 11x - \sqrt{11} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{11})[X]$ des nombres :

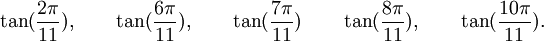
$\tan(\frac{2\pi}{11}), \qquad \tan(\frac{6\pi}{11}), \qquad \tan(\frac{7\pi}{11}) \qquad \tan(\frac{8\pi}{11}), \qquad \tan(\frac{10\pi}{11}). ~$

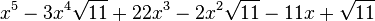
$x^5 - 3x^4\sqrt{11} + 22x^3 - 2x^2\sqrt{11} - 11x + \sqrt{11} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{11})[X]$ des nombres :

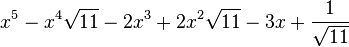
$x^5 - x^4\sqrt{11} - 2x^3 + 2x^2\sqrt{11} - 3x + \frac{1}{\sqrt{11}} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{11})[X]$ des nombres :

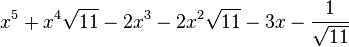
$x^5 + x^4\sqrt{11} - 2x^3 - 2x^2\sqrt{11} - 3x - \frac{1}{\sqrt{11}} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{11})[X]$ des nombres :

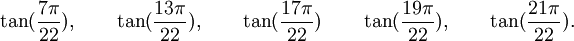
$\tan(\frac{7\pi}{22}), \qquad \tan(\frac{13\pi}{22}), \qquad \tan(\frac{17\pi}{22}) \qquad \tan(\frac{19\pi}{22}), \qquad \tan(\frac{21\pi}{22}). ~$

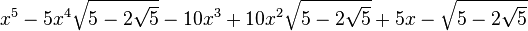
$x^5 - 5x^4\sqrt{5-2\sqrt{5}} - 10x^3 + 10x^2\sqrt{5-2\sqrt{5}} + 5x - \sqrt{5-2\sqrt{5}} ~$

Est le polynôme minimal dans $\mathbb{Q}\left(\sqrt{5},\sqrt{5-2\sqrt{5}},\sqrt{5+2\sqrt{5}},\sqrt{25-10\sqrt{5}},\sqrt{25+10\sqrt{5}}\right)[X]$ des nombres :

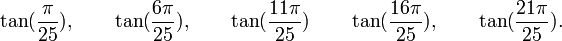
$\tan(\frac{\pi}{25}), \qquad \tan(\frac{6\pi}{25}), \qquad \tan(\frac{11\pi}{25}) \qquad \tan(\frac{16\pi}{25}), \qquad \tan(\frac{21\pi}{25}). ~$

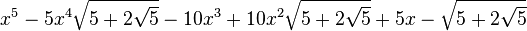
$x^5 - 5x^4\sqrt{5+2\sqrt{5}} - 10x^3 + 10x^2\sqrt{5+2\sqrt{5}} + 5x - \sqrt{5+2\sqrt{5}} ~$

Est le polynôme minimal dans $\mathbb{Q}\left(\sqrt{5},\sqrt{5-2\sqrt{5}},\sqrt{5+2\sqrt{5}},\sqrt{25-10\sqrt{5}},\sqrt{25+10\sqrt{5}}\right)[X]$ des nombres :

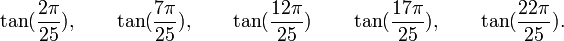
$\tan(\frac{2\pi}{25}), \qquad \tan(\frac{7\pi}{25}), \qquad \tan(\frac{12\pi}{25}) \qquad \tan(\frac{17\pi}{25}), \qquad \tan(\frac{22\pi}{25}). ~$

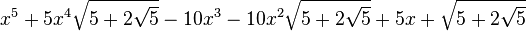
$x^5 + 5x^4\sqrt{5+2\sqrt{5}} - 10x^3 - 10x^2\sqrt{5+2\sqrt{5}} + 5x + \sqrt{5+2\sqrt{5}} ~$

Est le polynôme minimal dans $\mathbb{Q}\left(\sqrt{5},\sqrt{5-2\sqrt{5}},\sqrt{5+2\sqrt{5}},\sqrt{25-10\sqrt{5}},\sqrt{25+10\sqrt{5}}\right)[X]$ des nombres :

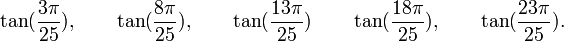
$\tan(\frac{3\pi}{25}), \qquad \tan(\frac{8\pi}{25}), \qquad \tan(\frac{13\pi}{25}) \qquad \tan(\frac{18\pi}{25}), \qquad \tan(\frac{23\pi}{25}). ~$

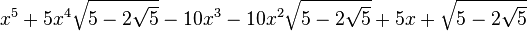
$x^5 + 5x^4\sqrt{5-2\sqrt{5}} - 10x^3 - 10x^2\sqrt{5-2\sqrt{5}} + 5x + \sqrt{5-2\sqrt{5}} ~$

Est le polynôme minimal dans $\mathbb{Q}\left(\sqrt{5},\sqrt{5-2\sqrt{5}},\sqrt{5+2\sqrt{5}},\sqrt{25-10\sqrt{5}},\sqrt{25+10\sqrt{5}}\right)[X]$ des nombres :

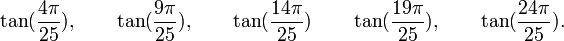
$\tan(\frac{4\pi}{25}), \qquad \tan(\frac{9\pi}{25}), \qquad \tan(\frac{14\pi}{25}) \qquad \tan(\frac{19\pi}{25}), \qquad \tan(\frac{24\pi}{25}). ~$

Etc...

Polynôme minimaux de nombres de la forme 2cos(kπ/n) ou 2sin(kπ/n).

🐋 Voici comment les déjections des baleines nous permettent de respirer

⏳ Ces édulcorants accéléreraient la puberté

👀 Découverte d'une multitude de trous noirs cachés dans l'Univers primordial

🌡️ Quelle est la température maximale que la Terre peut atteindre ?

💡 Cette nouvelle expérience montre qu'Einstein avait tort sur la lumière

🌵 Comment les plantes résistent-elles à la chaleur ?

👽 Sans le vouloir, nous communiquons notre position à d'éventuelles civilisations extraterrestres

📏 Les ancêtres humains avaient des 'hommes' bien plus grands que les 'femmes'

🧲 Une question résolue sur l'origine du champ magnétique terrestre

🍳 Ceci n'est pas un œuf, et il ne faut surtout pas le manger

🥔 La tomate: l'origine surprenante de nos pommes de terre

⛈️ Qu'est-ce que la foudre ?

🔵 Quel est le secret du bleu maya ?

🚨 L'obésité, un facteur de l'explosion des décès par cancer

🔭 Notre place dans l'Univers serait particulière, et cela explique bien des choses

🍉 Pourquoi les fruits d'été sont-ils si sucrés ?

🔭 Des forces cachées aux confins du Système solaire ?

🌍 Découverte de structures anciennes cachées sous l'Antarctique, et cela nous concerne directement

📢 Comment les cigales font-elles leur bruit ?

🌊 C'est énorme: 27 millions de tonnes de plastiques déversés dans l'Atlantique Nord

🔭 Cette observation suggère que tout pourrait venir de la ceinture d'astéroïdes

🦴 Comment les pythons digèrent-ils les os sans laisser de trace ?

💫 Comment un pulsar milliseconde a trompé les astronomes pendant des années ?

🌱 Par évolution dirigée, le MIT a fortement amélioré l'efficacité de la photosynthèse

🌍 Une météorite a-t-elle modifié le Grand Canyon il y a 56 000 ans ?

🕒 Le lien surprenant entre repas tardifs, santé et prise de poids

💥 Cette collision de trous noirs est si massive qu'elle fait trembler nos lois de l'astrophysique

🩺 Cancer: des cellules "oubliées" passent à l'offensive

🔭 Quel est cet objet mystérieux, lié à Neptune dans une orbite jamais vue auparavant ?

🍄 Découverte surprenante: vivre 25 ans de plus grâce aux "champignons magiques" ?

🩺 L'âge des premières règles est un indicateur de la santé à venir

⚛️ Cette découverte pourrait expliquer pourquoi notre Univers existe

🌋 Découverte majeure sous Yellowstone grâce à l'IA

🏹 Violence préhistorique: découverte d'un surprenant homicide raté

🌌 Des scientifiques découvrent dans l'Univers un gigantesque filament de matière "manquante"

🐱 Ce chat a aidé à découvrir un virus inconnu... deux fois !

🪐 Cette planète provoque la fureur de son étoile

👂 Et si nous pouvions entendre une caresse ?

👑 Cette découverte archéologique révèle les prémices des pharaons

🦈 Le requin bleu peut changer de couleur, comme un caméléon

🌞 La NASA dévoile les images les plus proches jamais prises du soleil

⏳ Il est maintenant possible de mesurer le vieillissement avec précision

🚀 1 pétabit/seconde: ce nouveau record permet de télécharger tout le catalogue de Netflix en 1 seconde

🩺 Donald Trump et insuffisance veineuse chronique: une maladie aux complications graves

🌍 Les barrages construits par l'Homme ont déplacé les pôles de la Terre

🍖 Les Néandertaliens avaient leurs propres recettes de cuisine, qui veut goûter ?

🔭 À l'observatoire Rubin, le grand film de l'Univers démarre

🧬 Réparer l'ADN cassé et sauver nos cellules

🪨 Découverte d'un important gisement de "kryptonite" en Europe, au potentiel énergétique hors norme

🕰️ La Terre possède sa propre horloge géologique

Page générée en 0.591 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise