Polynôme minimal trigonométrique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Polynôme minimaux de nombres de la forme 2cos(kπ/n) ou 2sin(kπ/n). - Formules générales en relation avec les coefficients des polynomes minimaux trigonométriques. - Polynômes minimaux de nombres de la forme tan(kπ/n).

Introduction

Les nombres de la forme :

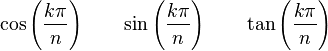
$\cos\left(\frac{k\pi}{n}\right) \qquad \sin\left(\frac{k\pi}{n}\right) \qquad \tan\left(\frac{k\pi}{n}\right)$

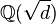
sont des nombres algébriques et à ce titre, ils admettent un polynôme minimal sur $\mathbb{Q}[X]$ . On obtient même des polynômes de degrés moindres en acceptant que les coefficients du polynôme appartiennent à un corps quadratique $\mathbb{Q}(\sqrt{d})$ . d étant un diviseur de n.

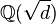
Dans cet article, on nommera donc $\mathbb{Q}(\sqrt{d})[X]$ l'ensemble des polynômes à coefficients dans le corps quadratique $\mathbb{Q}(\sqrt{d})$ .

Polynôme minimaux de nombres de la forme 2cos(kπ/n) ou 2sin(kπ/n).

Ci-dessous se trouvent, dans l'ordre des degrés croissants, les premiers polynômes minimaux des nombres de la forme 2.cos(k $π$ /n) ou de la forme 2.sin(k $π$ /n). Le facteur 2 n'est là que pour simplifier les coefficients du polynome.

Polynômes du premier degré

$x - 1 \qquad x + 1 \qquad x - 2 \qquad x + 2$

sont respectivement les polynômes minimaux des nombres :

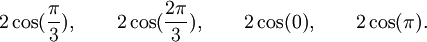
$2\cos(\frac{\pi}{3}), \qquad 2\cos(\frac{2\pi}{3}), \qquad 2\cos(0), \qquad 2\cos(\pi). ~$

Qui peuvent aussi se mettre sous la forme :

$2\sin(\frac{\pi}{6}), \qquad 2\sin(\frac{-\pi}{6}), \qquad 2\sin(\frac{\pi}{2}), \qquad 2\sin(\frac{-\pi}{2}). ~$

$x - \sqrt{2} \qquad x + \sqrt{2} \qquad x - \sqrt{3} \qquad x + \sqrt{3}$

sont respectivement les polynômes minimaux dans $\mathbb{Q}(\sqrt{2})[X]$ et $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

$2\cos(\frac{\pi}{4}), \qquad 2\cos(\frac{3\pi}{4}), \qquad 2\cos(\frac{\pi}{6}), \qquad 2\cos(\frac{5\pi}{6}). ~$

Qui peuvent aussi se mettre sous la forme :

$2\sin(\frac{\pi}{4}), \qquad 2\sin(\frac{-\pi}{4}), \qquad 2\sin(\frac{\pi}{3}), \qquad 2\sin(\frac{-\pi}{3}). ~$

Polynômes de second degré

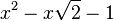
$x^2 - x\sqrt{2} - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{2})[X]$ des nombres :

$2\cos(\frac{\pi}{12}), \qquad 2\cos(\frac{7\pi}{12}). ~$

Qui peuvent aussi se mettre sous la forme :

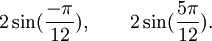
$2\sin(\frac{-\pi}{12}), \qquad 2\sin(\frac{5\pi}{12}). ~$

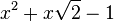
$x^2 + x\sqrt{2} - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{2})[X]$ des nombres :

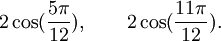
$2\cos(\frac{5\pi}{12}), \qquad 2\cos(\frac{11\pi}{12}). ~$

Qui peuvent aussi se mettre sous la forme :

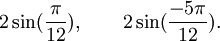
$2\sin(\frac{\pi}{12}), \qquad 2\sin(\frac{-5\pi}{12}). ~$

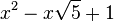
$x^2 - x\sqrt{5} + 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{5})[X]$ des nombres :

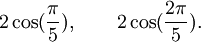
$2\cos(\frac{\pi}{5}), \qquad 2\cos(\frac{2\pi}{5}). ~$

Qui peuvent aussi se mettre sous la forme :

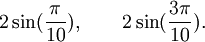
$2\sin(\frac{\pi}{10}), \qquad 2\sin(\frac{3\pi}{10}). ~$

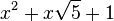
$x^2 + x\sqrt{5} + 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{5})[X]$ des nombres :

$2\cos(\frac{3\pi}{5}), \qquad 2\cos(\frac{4\pi}{5}). ~$

Qui peuvent aussi se mettre sous la forme :

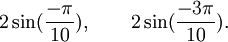
$2\sin(\frac{-\pi}{10}), \qquad 2\sin(\frac{-3\pi}{10}). ~$

Polynômes du troisième degré

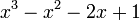
$x^3 - x^2 - 2x + 1 ~$

Est le polynôme minimal des nombres :

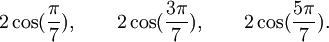
$2\cos(\frac{\pi}{7}), \qquad 2\cos(\frac{3\pi}{7}), \qquad 2\cos(\frac{5\pi}{7}). ~$

Qui peuvent aussi se mettre sous la forme :

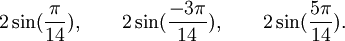
$2\sin(\frac{\pi}{14}), \qquad 2\sin(\frac{-3\pi}{14}), \qquad 2\sin(\frac{5\pi}{14}). ~$

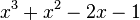
$x^3 + x^2 - 2x - 1 ~$

Est le polynôme minimal des nombres :

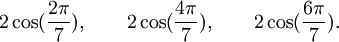
$2\cos(\frac{2\pi}{7}), \qquad 2\cos(\frac{4\pi}{7}), \qquad 2\cos(\frac{6\pi}{7}). ~$

Qui peuvent aussi se mettre sous la forme :

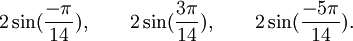
$2\sin(\frac{-\pi}{14}), \qquad 2\sin(\frac{3\pi}{14}), \qquad 2\sin(\frac{-5\pi}{14}). ~$

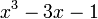
$x^3 - 3x - 1 ~$

Est le polynôme minimal des nombres :

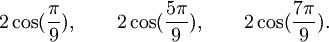
$2\cos(\frac{\pi}{9}), \qquad 2\cos(\frac{5\pi}{9}), \qquad 2\cos(\frac{7\pi}{9}). ~$

Qui peuvent aussi se mettre sous la forme :

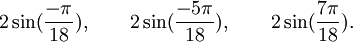
$2\sin(\frac{-\pi}{18}), \qquad 2\sin(\frac{-5\pi}{18}), \qquad 2\sin(\frac{7\pi}{18}). ~$

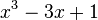
$x^3 - 3x + 1 ~$

Est le polynôme minimal des nombres :

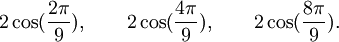
$2\cos(\frac{2\pi}{9}), \qquad 2\cos(\frac{4\pi}{9}), \qquad 2\cos(\frac{8\pi}{9}). ~$

Qui peuvent aussi se mettre sous la forme :

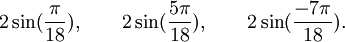
$2\sin(\frac{\pi}{18}), \qquad 2\sin(\frac{5\pi}{18}), \qquad 2\sin(\frac{-7\pi}{18}). ~$

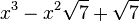
$x^3 - x^2\sqrt{7} + \sqrt{7} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{7})[X]$ des nombres :

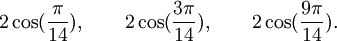
$2\cos(\frac{\pi}{14}), \qquad 2\cos(\frac{3\pi}{14}), \qquad 2\cos(\frac{9\pi}{14}). ~$

Qui peuvent aussi se mettre sous la forme :

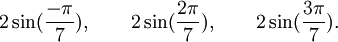
$2\sin(\frac{-\pi}{7}), \qquad 2\sin(\frac{2\pi}{7}), \qquad 2\sin(\frac{3\pi}{7}). ~$

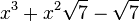
$x^3 + x^2\sqrt{7} - \sqrt{7} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{7})[X]$ des nombres :

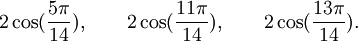
$2\cos(\frac{5\pi}{14}), \qquad 2\cos(\frac{11\pi}{14}), \qquad 2\cos(\frac{13\pi}{14}). ~$

Qui peuvent aussi se mettre sous la forme :

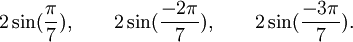
$2\sin(\frac{\pi}{7}), \qquad 2\sin(\frac{-2\pi}{7}), \qquad 2\sin(\frac{-3\pi}{7}). ~$

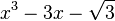
$x^3 - 3x - \sqrt{3} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

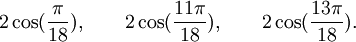
$2\cos(\frac{\pi}{18}), \qquad 2\cos(\frac{11\pi}{18}), \qquad 2\cos(\frac{13\pi}{18}). ~$

Qui peuvent aussi se mettre sous la forme :

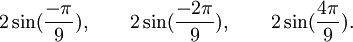
$2\sin(\frac{-\pi}{9}), \qquad 2\sin(\frac{-2\pi}{9}), \qquad 2\sin(\frac{4\pi}{9}). ~$

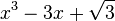
$x^3 - 3x + \sqrt{3} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

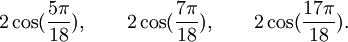
$2\cos(\frac{5\pi}{18}), \qquad 2\cos(\frac{7\pi}{18}), \qquad 2\cos(\frac{17\pi}{18}). ~$

Qui peuvent aussi se mettre sous la forme :

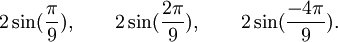
$2\sin(\frac{\pi}{9}), \qquad 2\sin(\frac{2\pi}{9}), \qquad 2\sin(\frac{-4\pi}{9}). ~$

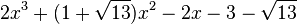
$2x^3 + (1 + \sqrt{13})x^2 - 2x - 3 - \sqrt{13} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{13})[X]$ des nombres :

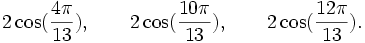
$2\cos(\frac{4\pi}{13}), \qquad 2\cos(\frac{10\pi}{13}), \qquad 2\cos(\frac{12\pi}{13}). ~$

Qui peuvent aussi se mettre sous la forme :

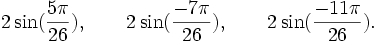
$2\sin(\frac{5\pi}{26}), \qquad 2\sin(\frac{-7\pi}{26}), \qquad 2\sin(\frac{-11\pi}{26}). ~$

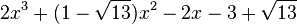
$2x^3 + (1 - \sqrt{13})x^2 - 2x - 3 + \sqrt{13} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{13})[X]$ des nombres :

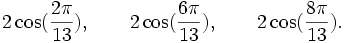
$2\cos(\frac{2\pi}{13}), \qquad 2\cos(\frac{6\pi}{13}), \qquad 2\cos(\frac{8\pi}{13}). ~$

Qui peuvent aussi se mettre sous la forme :

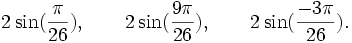
$2\sin(\frac{\pi}{26}), \qquad 2\sin(\frac{9\pi}{26}), \qquad 2\sin(\frac{-3\pi}{26}). ~$

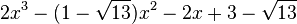
$2x^3 - (1 - \sqrt{13})x^2 - 2x + 3 - \sqrt{13} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{13})[X]$ des nombres :

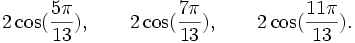
$2\cos(\frac{5\pi}{13}), \qquad 2\cos(\frac{7\pi}{13}), \qquad 2\cos(\frac{11\pi}{13}). ~$

Qui peuvent aussi se mettre sous la forme :

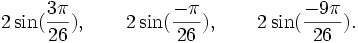
$2\sin(\frac{3\pi}{26}), \qquad 2\sin(\frac{-\pi}{26}), \qquad 2\sin(\frac{-9\pi}{26}). ~$

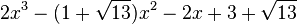
$2x^3 - (1 + \sqrt{13})x^2 - 2x + 3 + \sqrt{13} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{13})[X]$ des nombres :

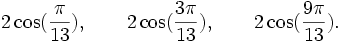
$2\cos(\frac{\pi}{13}), \qquad 2\cos(\frac{3\pi}{13}), \qquad 2\cos(\frac{9\pi}{13}). ~$

Qui peuvent aussi se mettre sous la forme :

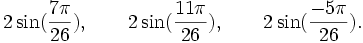
$2\sin(\frac{7\pi}{26}), \qquad 2\sin(\frac{11\pi}{26}), \qquad 2\sin(\frac{-5\pi}{26}). ~$

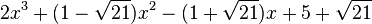
$2x^3 + (1 - \sqrt{21})x^2 - (1 + \sqrt{21})x + 5 + \sqrt{21} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{21})[X]$ des nombres :

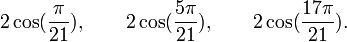
$2\cos(\frac{\pi}{21}), \qquad 2\cos(\frac{5\pi}{21}), \qquad 2\cos(\frac{17\pi}{21}). ~$

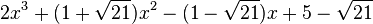
$2x^3 + (1 + \sqrt{21})x^2 - (1 - \sqrt{21})x + 5 - \sqrt{21} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{21})[X]$ des nombres :

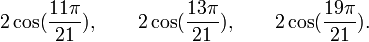
$2\cos(\frac{11\pi}{21}), \qquad 2\cos(\frac{13\pi}{21}), \qquad 2\cos(\frac{19\pi}{21}). ~$

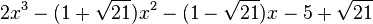
$2x^3 - (1 + \sqrt{21})x^2 - (1 - \sqrt{21})x - 5 + \sqrt{21} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{21})[X]$ des nombres :

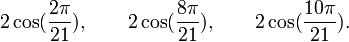
$2\cos(\frac{2\pi}{21}), \qquad 2\cos(\frac{8\pi}{21}), \qquad 2\cos(\frac{10\pi}{21}). ~$

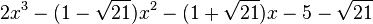
$2x^3 - (1 - \sqrt{21})x^2 - (1 + \sqrt{21})x - 5 - \sqrt{21} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{21})[X]$ des nombres :

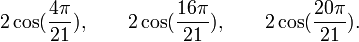
$2\cos(\frac{4\pi}{21}), \qquad 2\cos(\frac{16\pi}{21}), \qquad 2\cos(\frac{20\pi}{21}). ~$

Polynômes du quatrième degré

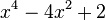
$x^4 - 4x^2 + 2 ~$

Est le polynôme minimal des nombres :

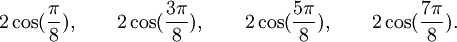
$2\cos(\frac{\pi}{8}), \qquad 2\cos(\frac{3\pi}{8}), \qquad 2\cos(\frac{5\pi}{8}), \qquad 2\cos(\frac{7\pi}{8}) . ~$

Qui peuvent aussi se mettre sous la forme :

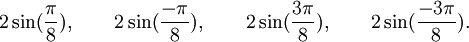
$2\sin(\frac{\pi}{8}), \qquad 2\sin(\frac{-\pi}{8}), \qquad 2\sin(\frac{3\pi}{8}), \qquad 2\sin(\frac{-3\pi}{8}) . ~$

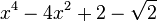
$x^4 - 4x^2 + 2 - \sqrt{2} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{2})[X]$ des nombres :

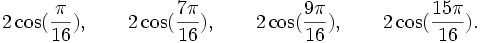
$2\cos(\frac{\pi}{16}), \qquad 2\cos(\frac{7\pi}{16}), \qquad 2\cos(\frac{9\pi}{16}), \qquad 2\cos(\frac{15\pi}{16}) . ~$

Qui peuvent aussi se mettre sous la forme :

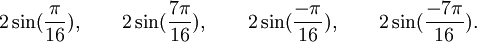
$2\sin(\frac{\pi}{16}), \qquad 2\sin(\frac{7\pi}{16}), \qquad 2\sin(\frac{-\pi}{16}), \qquad 2\sin(\frac{-7\pi}{16}) . ~$

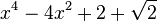
$x^4 - 4x^2 + 2 + \sqrt{2} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{2})[X]$ des nombres :

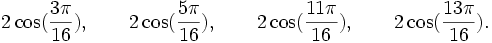
$2\cos(\frac{3\pi}{16}), \qquad 2\cos(\frac{5\pi}{16}), \qquad 2\cos(\frac{11\pi}{16}), \qquad 2\cos(\frac{13\pi}{16}) . ~$

Qui peuvent aussi se mettre sous la forme :

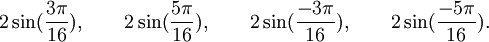
$2\sin(\frac{3\pi}{16}), \qquad 2\sin(\frac{5\pi}{16}), \qquad 2\sin(\frac{-3\pi}{16}), \qquad 2\sin(\frac{-5\pi}{16}) . ~$

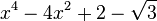
$x^4 - 4x^2 + 2 - \sqrt{3} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

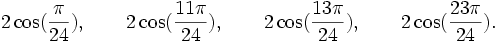
$2\cos(\frac{\pi}{24}), \qquad 2\cos(\frac{11\pi}{24}), \qquad 2\cos(\frac{13\pi}{24}), \qquad 2\cos(\frac{23\pi}{24}) . ~$

Qui peuvent aussi se mettre sous la forme :

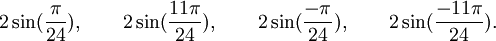
$2\sin(\frac{\pi}{24}), \qquad 2\sin(\frac{11\pi}{24}), \qquad 2\sin(\frac{-\pi}{24}), \qquad 2\sin(\frac{-11\pi}{24}) . ~$

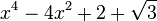
$x^4 - 4x^2 + 2 + \sqrt{3} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{3})[X]$ des nombres :

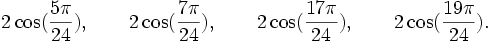
$2\cos(\frac{5\pi}{24}), \qquad 2\cos(\frac{7\pi}{24}), \qquad 2\cos(\frac{17\pi}{24}), \qquad 2\cos(\frac{19\pi}{24}) . ~$

Qui peuvent aussi se mettre sous la forme :

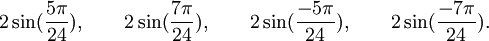
$2\sin(\frac{5\pi}{24}), \qquad 2\sin(\frac{7\pi}{24}), \qquad 2\sin(\frac{-5\pi}{24}), \qquad 2\sin(\frac{-7\pi}{24}) . ~$

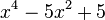
$x^4 - 5x^2 + 5 ~$

Est le polynôme minimal des nombres :

$2\cos(\frac{\pi}{10}), \qquad 2\cos(\frac{3\pi}{10}), \qquad 2\cos(\frac{7\pi}{10}), \qquad 2\cos(\frac{9\pi}{10}) . ~$

Qui peuvent aussi se mettre sous la forme :

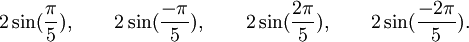
$2\sin(\frac{\pi}{5}), \qquad 2\sin(\frac{-\pi}{5}), \qquad 2\sin(\frac{2\pi}{5}), \qquad 2\sin(\frac{-2\pi}{5}) . ~$

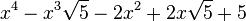
$x^4 - x^3\sqrt{5} - 2x^2 + 2x\sqrt{5} + 5 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{5})[X]$ des nombres :

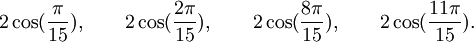
$2\cos(\frac{\pi}{15}), \qquad 2\cos(\frac{2\pi}{15}), \qquad 2\cos(\frac{8\pi}{15}), \qquad 2\cos(\frac{11\pi}{15}) . ~$

Qui peuvent aussi se mettre sous la forme :

$2\sin(\frac{-\pi}{30}), \qquad 2\sin(\frac{-7\pi}{30}), \qquad 2\sin(\frac{11\pi}{30}), \qquad 2\sin(\frac{13\pi}{30}) . ~$

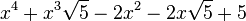
$x^4 + x^3\sqrt{5} - 2x^2 - 2x\sqrt{5} + 5 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{5})[X]$ des nombres :

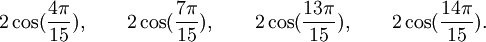
$2\cos(\frac{4\pi}{15}), \qquad 2\cos(\frac{7\pi}{15}), \qquad 2\cos(\frac{13\pi}{15}), \qquad 2\cos(\frac{14\pi}{15}) . ~$

Qui peuvent aussi se mettre sous la forme :

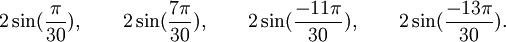
$2\sin(\frac{\pi}{30}), \qquad 2\sin(\frac{7\pi}{30}), \qquad 2\sin(\frac{-11\pi}{30}), \qquad 2\sin(\frac{-13\pi}{30}) . ~$

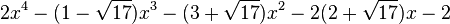
$2x^4 - (1 - \sqrt{17})x^3 - (3 + \sqrt{17})x^2 - 2(2 + \sqrt{17})x - 2 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{17})[X]$ des nombres :

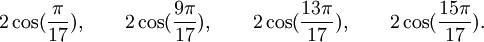
$2\cos(\frac{\pi}{17}), \qquad 2\cos(\frac{9\pi}{17}), \qquad 2\cos(\frac{13\pi}{17}), \qquad 2\cos(\frac{15\pi}{17}) . ~$

Qui peuvent aussi se mettre sous la forme :

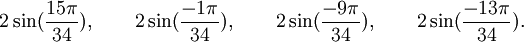
$2\sin(\frac{15\pi}{34}), \qquad 2\sin(\frac{-1\pi}{34}), \qquad 2\sin(\frac{-9\pi}{34}), \qquad 2\sin(\frac{-13\pi}{34}) . ~$

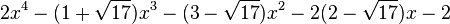
$2x^4 - (1 + \sqrt{17})x^3 - (3 - \sqrt{17})x^2 - 2(2 - \sqrt{17})x - 2 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{17})[X]$ des nombres :

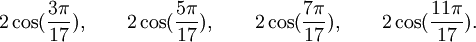
$2\cos(\frac{3\pi}{17}), \qquad 2\cos(\frac{5\pi}{17}), \qquad 2\cos(\frac{7\pi}{17}), \qquad 2\cos(\frac{11\pi}{17}) . ~$

Qui peuvent aussi se mettre sous la forme :

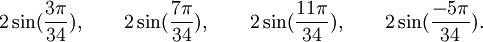
$2\sin(\frac{3\pi}{34}), \qquad 2\sin(\frac{7\pi}{34}), \qquad 2\sin(\frac{11\pi}{34}), \qquad 2\sin(\frac{-5\pi}{34}) . ~$

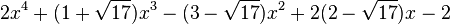
$2x^4 + (1 + \sqrt{17})x^3 - (3 - \sqrt{17})x^2 + 2(2 - \sqrt{17})x - 2 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{17})[X]$ des nombres :

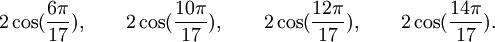
$2\cos(\frac{6\pi}{17}), \qquad 2\cos(\frac{10\pi}{17}), \qquad 2\cos(\frac{12\pi}{17}), \qquad 2\cos(\frac{14\pi}{17}) . ~$

Qui peuvent aussi se mettre sous la forme :

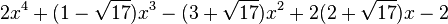
$2x^4 + (1 - \sqrt{17})x^3 - (3 + \sqrt{17})x^2 + 2(2 + \sqrt{17})x - 2 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{17})[X]$ des nombres :

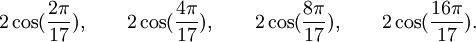
$2\cos(\frac{2\pi}{17}), \qquad 2\cos(\frac{4\pi}{17}), \qquad 2\cos(\frac{8\pi}{17}), \qquad 2\cos(\frac{16\pi}{17}) . ~$

Qui peuvent aussi se mettre sous la forme :

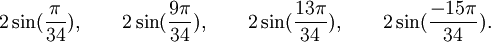
$2\sin(\frac{\pi}{34}), \qquad 2\sin(\frac{9\pi}{34}), \qquad 2\sin(\frac{13\pi}{34}), \qquad 2\sin(\frac{-15\pi}{34}) . ~$

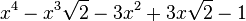
$x^4 - x^3\sqrt{2} - 3x^2 + 3x\sqrt{2} - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{2})[X]$ des nombres :

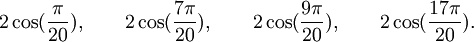
$2\cos(\frac{\pi}{20}), \qquad 2\cos(\frac{7\pi}{20}), \qquad 2\cos(\frac{9\pi}{20}), \qquad 2\cos(\frac{17\pi}{20}) . ~$

Qui peuvent aussi se mettre sous la forme :

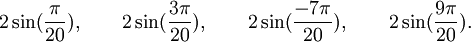
$2\sin(\frac{\pi}{20}), \qquad 2\sin(\frac{3\pi}{20}), \qquad 2\sin(\frac{-7\pi}{20}), \qquad 2\sin(\frac{9\pi}{20}) . ~$

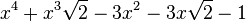
$x^4 + x^3\sqrt{2} - 3x^2 - 3x\sqrt{2} - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{2})[X]$ des nombres :

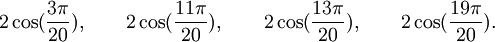
$2\cos(\frac{3\pi}{20}), \qquad 2\cos(\frac{11\pi}{20}), \qquad 2\cos(\frac{13\pi}{20}), \qquad 2\cos(\frac{19\pi}{20}) . ~$

Qui peuvent aussi se mettre sous la forme :

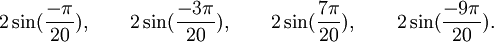
$2\sin(\frac{-\pi}{20}), \qquad 2\sin(\frac{-3\pi}{20}), \qquad 2\sin(\frac{7\pi}{20}), \qquad 2\sin(\frac{-9\pi}{20}) . ~$

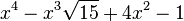
$x^4 - x^3\sqrt{15} + 4x^2 - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{15})[X]$ des nombres :

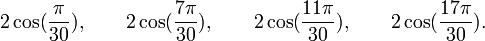
$2\cos(\frac{\pi}{30}), \qquad 2\cos(\frac{7\pi}{30}), \qquad 2\cos(\frac{11\pi}{30}), \qquad 2\cos(\frac{17\pi}{30}) . ~$

Qui peuvent aussi se mettre sous la forme :

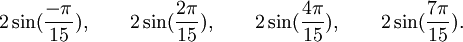
$2\sin(\frac{-\pi}{15}), \qquad 2\sin(\frac{2\pi}{15}), \qquad 2\sin(\frac{4\pi}{15}), \qquad 2\sin(\frac{7\pi}{15}) . ~$

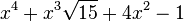
$x^4 + x^3\sqrt{15} + 4x^2 - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{15})[X]$ des nombres :

$2\cos(\frac{13\pi}{30}), \qquad 2\cos(\frac{19\pi}{30}), \qquad 2\cos(\frac{23\pi}{30}), \qquad 2\cos(\frac{29\pi}{30}) . ~$

Qui peuvent aussi se mettre sous la forme :

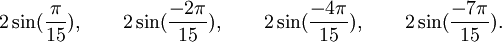
$2\sin(\frac{\pi}{15}), \qquad 2\sin(\frac{-2\pi}{15}), \qquad 2\sin(\frac{-4\pi}{15}), \qquad 2\sin(\frac{-7\pi}{15}) . ~$

Polynômes du cinquième degré

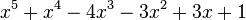
$x^5 + x^4 - 4x^3 - 3x^2 + 3x + 1 ~$

Est le polynôme minimal des nombres :

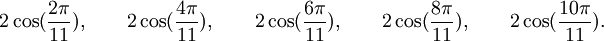
$2\cos(\frac{2\pi}{11}), \qquad 2\cos(\frac{4\pi}{11}), \qquad 2\cos(\frac{6\pi}{11}), \qquad 2\cos(\frac{8\pi}{11}), \qquad 2\cos(\frac{10\pi}{11}). ~$

Qui peuvent aussi se mettre sous la forme :

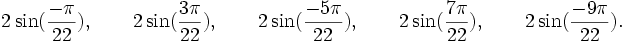
$2\sin(\frac{-\pi}{22}), \qquad 2\sin(\frac{3\pi}{22}), \qquad 2\sin(\frac{-5\pi}{22}), \qquad 2\sin(\frac{7\pi}{22}), \qquad 2\sin(\frac{-9\pi}{22}). ~$

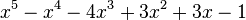
$x^5 - x^4 - 4x^3 + 3x^2 + 3x - 1 ~$

Est le polynôme minimal des nombres :

Qui peuvent aussi se mettre sous la forme :

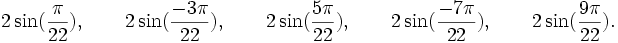
$2\sin(\frac{\pi}{22}), \qquad 2\sin(\frac{-3\pi}{22}), \qquad 2\sin(\frac{5\pi}{22}), \qquad 2\sin(\frac{-7\pi}{22}), \qquad 2\sin(\frac{9\pi}{22}). ~$

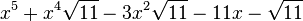
$x^5 + x^4\sqrt{11} - 3x^2\sqrt{11} - 11x - \sqrt{11} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{11})[X]$ des nombres :

Qui peuvent aussi se mettre sous la forme :

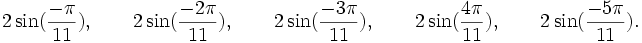
$2\sin(\frac{-\pi}{11}), \qquad 2\sin(\frac{-2\pi}{11}), \qquad 2\sin(\frac{-3\pi}{11}), \qquad 2\sin(\frac{4\pi}{11}), \qquad 2\sin(\frac{-5\pi}{11}) . ~$

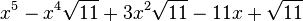
$x^5 - x^4\sqrt{11} + 3x^2\sqrt{11} - 11x + \sqrt{11} ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{11})[X]$ des nombres :

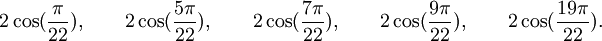
$2\cos(\frac{\pi}{22}), \qquad 2\cos(\frac{5\pi}{22}), \qquad 2\cos(\frac{7\pi}{22}), \qquad 2\cos(\frac{9\pi}{22}), \qquad 2\cos(\frac{19\pi}{22}) . ~$

Qui peuvent aussi se mettre sous la forme :

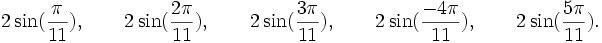
$2\sin(\frac{\pi}{11}), \qquad 2\sin(\frac{2\pi}{11}), \qquad 2\sin(\frac{3\pi}{11}), \qquad 2\sin(\frac{-4\pi}{11}), \qquad 2\sin(\frac{5\pi}{11}). ~$

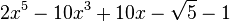
$2x^5 - 10x^3 + 10x - \sqrt{5} - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{5})[X]$ des nombres :

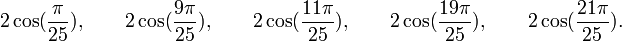
$2\cos(\frac{\pi}{25}), \qquad 2\cos(\frac{9\pi}{25}), \qquad 2\cos(\frac{11\pi}{25}), \qquad 2\cos(\frac{19\pi}{25}), \qquad 2\cos(\frac{21\pi}{25}) . ~$

Qui peuvent aussi se mettre sous la forme :

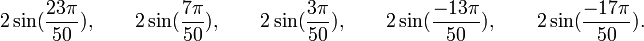
$2\sin(\frac{23\pi}{50}), \qquad 2\sin(\frac{7\pi}{50}), \qquad 2\sin(\frac{3\pi}{50}), \qquad 2\sin(\frac{-13\pi}{50}), \qquad 2\sin(\frac{-17\pi}{50}). ~$

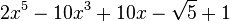
$2x^5 - 10x^3 + 10x - \sqrt{5} + 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{5})[X]$ des nombres :

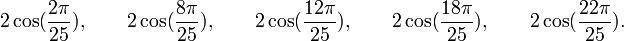
$2\cos(\frac{2\pi}{25}), \qquad 2\cos(\frac{8\pi}{25}), \qquad 2\cos(\frac{12\pi}{25}), \qquad 2\cos(\frac{18\pi}{25}), \qquad 2\cos(\frac{22\pi}{25}) . ~$

Qui peuvent aussi se mettre sous la forme :

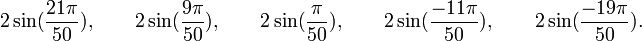
$2\sin(\frac{21\pi}{50}), \qquad 2\sin(\frac{9\pi}{50}), \qquad 2\sin(\frac{\pi}{50}), \qquad 2\sin(\frac{-11\pi}{50}), \qquad 2\sin(\frac{-19\pi}{50}). ~$

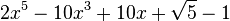
$2x^5 - 10x^3 + 10x + \sqrt{5} - 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{5})[X]$ des nombres :

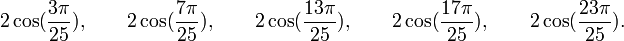
$2\cos(\frac{3\pi}{25}), \qquad 2\cos(\frac{7\pi}{25}), \qquad 2\cos(\frac{13\pi}{25}), \qquad 2\cos(\frac{17\pi}{25}), \qquad 2\cos(\frac{23\pi}{25}) . ~$

Qui peuvent aussi se mettre sous la forme :

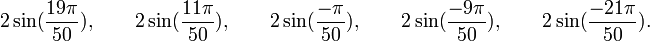
$2\sin(\frac{19\pi}{50}), \qquad 2\sin(\frac{11\pi}{50}), \qquad 2\sin(\frac{-\pi}{50}), \qquad 2\sin(\frac{-9\pi}{50}), \qquad 2\sin(\frac{-21\pi}{50}). ~$

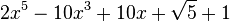
$2x^5 - 10x^3 + 10x + \sqrt{5} + 1 ~$

Est le polynôme minimal dans $\mathbb{Q}(\sqrt{5})[X]$ des nombres :

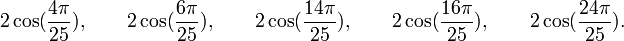
$2\cos(\frac{4\pi}{25}), \qquad 2\cos(\frac{6\pi}{25}), \qquad 2\cos(\frac{14\pi}{25}), \qquad 2\cos(\frac{16\pi}{25}), \qquad 2\cos(\frac{24\pi}{25}) . ~$

Qui peuvent aussi se mettre sous la forme :

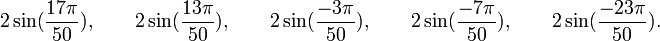
$2\sin(\frac{17\pi}{50}), \qquad 2\sin(\frac{13\pi}{50}), \qquad 2\sin(\frac{-3\pi}{50}), \qquad 2\sin(\frac{-7\pi}{50}), \qquad 2\sin(\frac{-23\pi}{50}). ~$

Etc...

Formules générales en relation avec les coefficients des polynomes minimaux trigonométriques.

Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭

Le rôle surprenant de la grossesse contre la grippe A 🦠

Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️

Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋

Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬

Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️

Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️

Ce nouveau type de moteur repousse les limites du vol supersonique ✈️

Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠

Une super-Terre entre Mars et Jupiter ? 🌎

Découverte impressionnante d'un fossile de crocodile géant 🐊

Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡

Un virage technologique révèle l'impact du diabète gestationnel 🩺

Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼

Ce fin gilet robotisé soulage les tâches répétitives 🦾

Les équations d'Einstein invalidées ? 👀

Ce tatouage électronique se connecte à votre cerveau 🧠

Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️

Des plats au bœuf... sans bœuf ? 🥩

Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍

Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️

Découverte: d'autres univers plus propices à la vie que le notre 👽

Ces sons urbains qui minent notre santé mentale 🚗

La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥

Des microalgues éliminent les métaux lourds: voici comment 🧪

Et voici un qubit mécanique ! 🖥️

Les lentilles de contact sont-elles vraiment sans danger ? 👁️

Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥

Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠

Cette astuce quotidienne ajoute 11 ans à votre vie 🕒

Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋

Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀

Voici pourquoi l'alcool peut rendre agressif 🥂

Expérience inédite: ce laser projette une ombre visible 💥

Ce plat millénaire réduit significativement la graisse corporelle 🍽️

Les scientifiques trompés ? La Voie Lactée n'est PAS comme les autres galaxies 🔭

Pourquoi ce que pensent les autres de nous nous fait tant ruminer ? 🧠

De la vie découverte sur un échantillon de l'astéroïde Ryugu (oups) 👽

Des anomalies incompréhensibles de températures détectées simultanément presque partout sur Terre 🌡️

Cette planète, trop jeune pour exister, bouscule les lois de l'astronomie 🪐

Une montagne d'or découverte en Chine ⛏️

Cette simulation de l'Univers est totalement vertigineuse 🌀

Une pilule pourrait-elle imiter les bienfaits du yoga ? 🧘

Nous serions-nous trompés sur l'origine de l'écriture alphabétique ? ✍️

Voici pourquoi votre enfant triche et ce que cela révèle 🧠

Le Sahara verdit, et cela pourrait bien (re)changer notre climat 🌱

Neuralink: un bras robotique contrôlé par la pensée 🦾

Ces fossiles humains à grands crânes seraient-ils une espèce jusqu'alors inconnue ? 💀

L'étonnant impact du froid sur notre sommeil ❄️

Une base cachée de missiles nucléaires repérée par erreur sous la calotte glacière ☢️

Page générée en 0.339 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise