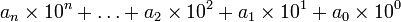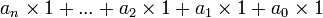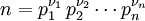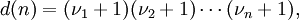Diviseur - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, un nombre entier d est un diviseur d'un entier n lorsque la division euclidienne de n par d donne un reste égal à zéro. Autrement dit, il existe un entier q tel que n = d × q.
Par exemple, 7 est un diviseur de 42 parce que 42/7 = 6. Nous disons aussi 42 est divisible par 7 ou 42 est un multiple de 7 ou 7 divise 42 et nous écrivons généralement 7 | 42. Les diviseurs peuvent être positifs ou négatifs. Les diviseurs positifs de 42 sont {1, 2, 3, 6, 7, 14, 21, 42}.
Certains cas spéciaux : 1 et -1 sont les diviseurs de chaque entier, et chaque entier est un diviseur de 0. Les nombres divisibles par 2 sont appelés pairs et ceux qui ne le sont pas sont appelés impairs.
Le nom vient de l'opération arithmétique de division : si a, b sont des entiers avec b non nul, et si a/b=c est un entier, alors a est le dividende, b le diviseur, et c le quotient.
Critères pour les petits diviseurs
Il existe certaines règles qui permettent de reconnaître les petits diviseurs d'un nombre à partir du nombre de ses chiffres décimaux.
Un critère de divisibilité est un critère que vous pouvez utiliser pour déterminer la divisibilité d'un nombre par un autre nombre. Ceux-ci sont basés sur les congruences modulo le diviseur cherché.
Par exemple, en système décimal, nous voulons savoir le critère pour le diviseur 3.
10 est congru à 1 modulo 3, 100 est congru à 1 modulo 3,...,10n est congru à 1 modulo 3
Un nombre en système décimal s'écrivant
est congru modulo 3 à
c’est-à-dire à la somme des coefficients des puissances de 10, c’est-à-dire la somme des chiffres qui composent le nombre. Cette somme doit être divisible par 3 pour que le nombre soit divisible par 3.
Diviseurs dans un anneau
Dans un anneau commutatif intègre A, un diviseur d'un élément
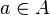
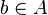
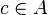
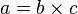
Notions supplémentaires et résultats
Quelques propriétés élémentaires :
- Si a divise b et a divise c, alors a divise (bx+cy).
- Si a divise b et b divise c, alors a divise c.
- Si a divise b et b divise a, alors a=b ou a=-b.
Tout nombre entier n possède pour diviseurs triviaux positifs, 1 et lui-même.
Un diviseur positif de n, différent de n et 1, est appelé un diviseur propre (ou diviseur strict, ou une partie aliquote) de n. Un nombre qui ne divise pas également n, mais qui laisse un reste, est appelé une partie aliquante de n.
Un nombre entier n > 1 qui ne possède pas de diviseur propre est appelé un nombre premier. (Les nombres 0 et 1 ne sont pas premiers.)
N'importe quel diviseur de n est le produit de diviseurs premiers de n avec une certaine puissance en exposant. Ceci est une conséquence du théorème fondamental de l'arithmétique.
Si un nombre est égal à la somme de ses diviseurs stricts, il est appelé un nombre parfait. Les nombres inférieurs à cette somme sont dits déficients, alors que les nombres plus grands que cette somme sont dits abondants.
Le nombre total de diviseurs propres de n est une fonction multiplicative d(n) (par exemple :
-
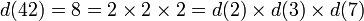
La somme des diviseurs propres de n est une autre fonction multiplicative
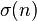
-
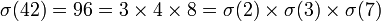
La relation « divise » munit l'ensemble N des nombres entiers positifs d'une relation d'ordre partiel, qui en fait même un treillis complet. Le plus grand élément de ce treillis est 0 et le plus petit est 1. L'opération binaire de borne inférieure
Si un nombre entier n est écrit dans une base b, et d est un nombre entier avec b ≡ 1 (mod d), alors n est divisible par d si et seulement si la somme de ses chiffres est divisible par d. Le critère donné pour d=3 donné plus haut est un cas particulier de ce résultat. (b=10).
Si la décomposition en facteurs premiers de n est donnée par
alors le nombre de diviseurs positifs de n est
et chaque diviseur est de la forme
où