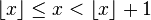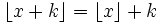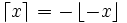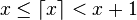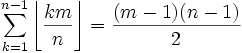Partie entière - Définition
En mathématiques, la fonction partie entière est la fonction définie de la manière suivante :
- Pour tout nombre réel x, la partie entière notée E(x) est le plus grand entier relatif inférieur ou égal à x.
- Par exemple : E(2,3) = 2, E(−2) = −2 et E(−2,3) = −3.
La fonction partie entière est aussi notée
![\left[ x \right]](https://static.techno-science.net/illustration/Definitions/autres/4/4fcbf9b418b2ad4ef36169fb15a32bdd_f256889fc33f431bc0dc2317a9455dbc.png)
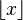
On a toujours :
avec égalité si et seulement si x est un entier relatif.
Pour tout entier relatif k et et pour tout nombre réel x, on a
L’arrondi à l’entier le plus proche d’un réel x peut être exprimé par E(x + 0,5).
La fonction partie entière n’est pas continue, mais est continue à droite. En fait elle est constante sur tout intervalle de la forme [k, k+1[ et n’est pas continue en les entiers relatifs.
Une autre fonction mathématique du même type est la fonction " plafond " ou partie entière par excès ou partie entière supérieure (ceiling en anglais), définie de la manière suivante :
- Pour tout nombre réel x donné, plafond de x noté P(x) est le plus petit entier supérieur ou égal à x.
- Par exemple : P(2,3) = 3, P(2) = 2 et P(−2,3) = −2.
La fonction plafond est aussi notée
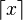
Il est facile de montrer que :
et que :
Pour tout entier relatif k, on a aussi l’égalité suivante :
-
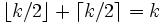
Si m et n sont des entiers naturels premiers entre eux alors