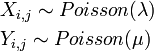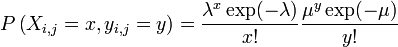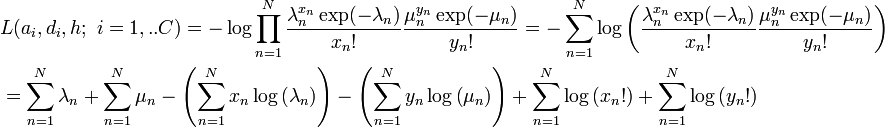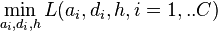Prédiction statistique des résultats de football - Définition

Time Independent Poisson Regression

Selon ce modèle (Maher), si X_i,j et Y_i,j sont les buts marqués dans le match opposant l'équipe i à l'équipe j, alors:

X_i,j et Y_i,j sont des variables aléatoires indépendantes avec des moyennes arithmétiques λ et μ. Ainsi, la probabilité conjointe pour l'équipe à domicile de marquer x buts et pour l'équipe à l'extérieur de marquer y buts est un produit des deux probabilités indépendantes:

tandis que le modèle log-linéaire généralisé pour λ et μ d'après Kuonen et Lee est défini par: et , où a_i,d_i,h > 0 se réfèrent à la forece d'attaque, de défense et à l'avantage du terrain, respectivement. c^λ et c^μ sont des facteurs de correction qui représentent le nombre moyens de buts marqués au cours de la saison par l'équipe à domicile et à l'extérieur respectivement.

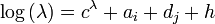
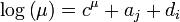
En supposant que C signifie le nombre d'équipes participant à une saison et que N représente le nombre de matches disputés jusqu'à présent, les forces d'une équipe peuvent être estimées en minimisant la fonction de log-vraisemblance négative par rapport à λ et μ:

Étant donné que x_n et y_n sont connus, les forces d'attaque et de défense de l'équipe et l'avantage du terrain qui minimisent la log-vraisemblance négative peuvent être estimés par l'Algorithme espérance-maximisation:

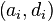
Des améliorations de ce modèle ont été suggérées par Mark Dixon et Stuart Coles. Ils ont inventé un facteur de corrélation pour les scores faibles 0-0, 1-0, 0-1 et 1-1, où l'hypothèse de Loi de Poisson indépendantes ne tient pas. Dimitris Karlis et Ioannis Ntzoufras ont construit un modèle Time-Independent Skellam Distribution. Contrairement au modèle de Poisson qui correspond à la distribution des scores, le modèle Skellam correspond à la différence entre les scores à domicile et à l'extérieur.