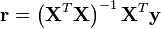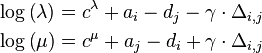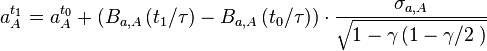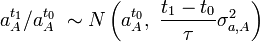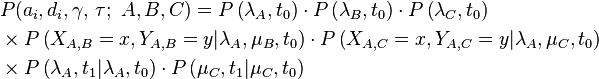Prédiction statistique des résultats de football - Définition
La liste des auteurs de cet article est disponible ici.
Time Independent Least Squares Rating
Cette méthode attribue à chaque équipe du tournoi une notation en continu, de sorte que la meilleure équipe aura la meilleure note. La méthode est basée sur l'hypothèse que la cote attribuée à l'équipe rivale est proportionnelle à l'issue de chaque match.
Supposons que les équipes A, B, C et D jouent dans un tournoi et que les résultats des matchs sont les suivants:
-
Match # Equipe à domicile Score Equipe à l'extérieur Y 1 A 3 - 1 B y1 = 3 − 1 2 C 2 - 1 D y2 = 2 − 1 3 D 1 - 4 B y3 = 1 − 4 4 A 3 - 1 D y4 = 3 − 1 5 B 2 - 0 C y5 = 2 − 0
Bien que les rangs rA, rB, rC et rD des équipes A, B, C et D, respectivement ne sont pas connus, on peut supposer que le résultat du match #1 est proportionnel à la différence entre les rangs des équipes A et B:
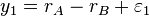
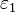
En introduisant une matrice de sélection X, les équations ci-dessus peut être réécrit sous une forme compacte:
-
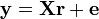
Les entrées de la matrice de sélection peut être soit 1, 0 ou -1, avec 1 correspondant à des équipes d'accueil et de -1 à l'écart des équipes:
Si la matrice
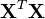
Les paramètres de la cote finale sont
![\mathbf{r}=[1,625, \ 0,75, \ -0,875, \ -1,5]^{T}](https://static.techno-science.net/illustration/Definitions/autres/6/6c02d67c14d09c49dea806e08342c857_e553bf1fd073f5621abc6fbcf4db8af0.png)
Méthodes de prévision
Toutes les méthodes de prédiction peuvent être classés selon le type de tournoi, le dépendance au temps et l'algorithme de régression utilisé. Les méthodes de prévision du football diffèrent entre championnat et tournoi à élimination directe. Les méthodes de prévision pour les tournoi à élimination directe sont résumées dans un article par Diego Kuonen.
Le tableau ci-dessous résume les méthodes utilisées pour les championnat.
-
# Code Méthode de Prévision Algorithme de régression Dépendance au temps Performance 1. TILS Time Independent Least Squares Rating Régression des moindres carrés linéaire N Faible 2. TIPR Time Independent Poisson Regression Maximum de vraisemblance N Moyenne 3. TISR Time Independent Skellam Regression Maximum de vraisemblance N Moyenne 4. TDPR Time Dependent Poisson Regression Maximum de vraisemblance Facteur d'amortissement du temps Haute 5. TDMC Time Dependant Markov Chain Monte-Carlo Chaîne de Markov Haute
Time Dependant Markov Chain
D'une part, les modèles statistiques nécessitent un grand nombre d'observations pour faire une estimation précise de ses paramètres. Et quand il n'y a pas suffisamment d'observations disponibles au cours d'une saison (comme c'est généralement le cas), travailler avec des statistiques moyennes a un sens. D'autre part, il est bien connu que les compétences des équipes changent au cours de la saison, ce qui rend les paramètres du modèle dépendant du temps. Mark Dixon et Stuart Coles ont essayé de résoudre ce problème par un compromis en attribuant un plus grand poids aux résultats du dernier match. Rue et Salvesen ont introduit une méthode de notation dépendant du temps en utilisant un modèle de chaînes de Markov.
Ils ont suggéré de modifier le modèle linéaire généralisé ci-dessus pour λ et μ:
étant donné que
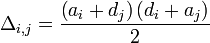
Selon le modèle, la force d'attaque
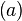
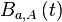
où τ et
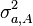
Ce modèle est basé sur l'hypothèse que:
En supposant que trois équipes A, B et C jouent dans le tournoi et que les matchs sont joués dans l'ordre suivant: t0: A-B; t0: A-C; t1: B-C, la densité de probabilité conjointe peut être exprimée comme suit:
Puisque l'estimation analytique des paramètres est difficile dans ce cas, la méthode de Monte Carlo est appliquée pour estimer les paramètres du modèle.
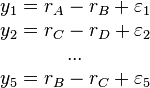
![\begin{matrix} \mathbf{y}=\left[ \begin{matrix} 2 \\ 1 \\ -3 \\ 2 \\ 2 \\ \end{matrix} \right], & \mathbf{X}= \left[ \begin{matrix} 1 & -1 & 0 & 0 \\ 0 & 0 & 1 & -1 \\ 0 & -1 & 0 & 1 \\ 1 & 0 & 0 & -1 \\ 0 & 1 & -1 & 0 \\ \end{matrix} \right], & \mathbf{r}=\left[ \begin{matrix} r_{A} \\ r_{B} \\ r_{C} \\ r_{D} \\ \end{matrix} \right], & \mathbf{e} = \left[ \begin{matrix} \varepsilon _{1} \\ \varepsilon _{2} \\ \varepsilon _{3} \\ \varepsilon _{4} \\ \varepsilon _{5} \\ \end{matrix} \right] \\ \end{matrix}](https://static.techno-science.net/illustration/Definitions/autres/9/9706646a818d5467e62a4d2f58d8ed4b_2c867f661ce90f3a0b627480404b806c.png)