Principe fondamental de la dynamique - Définition
La liste des auteurs de cet article est disponible ici.
Démonstration (mécanique quantique)
Les postulats de la mécanique quantique permettent de retrouver la deuxième loi de Newton. En partant du théorème d'Ehrenfest, qui affirme que l'évolution temporelle de la valeur moyenne
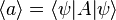
![\frac{d \langle a \rangle}{dt} = \frac{1}{i \hbar} \langle \psi |[ A,H] | \psi \rangle + \langle \psi | \frac{\partial A}{\partial t} | \psi \rangle](https://static.techno-science.net/illustration/Definitions/autres/2/22b22890a421f32bfdddc70f9cb8f268_607ddf3b476bd5b4529ac048ec9abb1d.png)
On applique ce théorème aux observables position et impulsion, dans le cas d'un hamiltonien
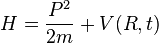
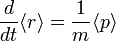
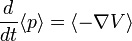
(ces relations sont démontrées en détail dans l'article théorème d'Ehrenfest).
En combinant les deux équations obtenues, on a
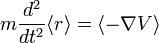
Cette relation correspond bien à l'équation de Newton si
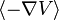
![\langle \nabla V\rangle = [\nabla V]_{\mathbf r = \langle r\rangle }](https://static.techno-science.net/illustration/Definitions/autres/4/4c00ce90f1af4c7a009923d05770c9df_051593d3aac733864489f9dba4e7601b.png)
Or,
![\begin{align} \langle \nabla V\rangle & = \langle \psi | \nabla V | \psi \rangle \\ \ & = \int \mathrm d^3 \mathbf r \;\psi^* \;\nabla V \;\psi \\ \ & = \int \mathrm d^3 \mathbf r \; |\psi|^2 \;\nabla V \\ \ & \simeq [\nabla V]_{\mathbf r = \langle r\rangle } \;\int \mathrm d^3 \mathbf r \; |\psi|^2 \\ \ & = [\nabla V]_{\mathbf r = \langle r\rangle } \end{align}](https://static.techno-science.net/illustration/Definitions/autres/9/9e37524e035e2d71fabd0d674a7d10fd_4e43c63d6488b0c2fd0c7eedd917699b.png)
si le paquet d'onde est suffisamment localisé, ce qui est le cas à l'échelle macroscopique. On a donc bien démontré la deuxième loi de Newton à partir des postulats de la mécanique quantique, et en particulier à partir de l'équation de Schrödinger (à travers le théorème d'Ehrenfest).
Référentiels non-galiléens
Notons enfin qu'il est possible de reformuler de manière plus large la deuxième loi de Newton dans un référentiel non galiléen en ajoutant des termes dans l'équation qui sont homogènes à des forces, et qu'on appelle souvent « forces d'inertie ». Ces termes ne sont pas des forces au sens usuel mais des termes correctifs d'origine géométrique et cinématique.

















































