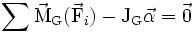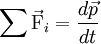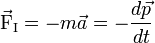Principe fondamental de la dynamique - Définition

Introduction

Le principe fondamental de la dynamique, ou PFD, dérive de la deuxième loi de Newton. On parle aussi parfois de la relation fondamentale de la dynamique, ou RFD. On peut aussi le voir comme découlant du principe des puissances virtuelles qui en est une formulation duale.

Principe fondamental de la dynamique en translation

Il s'agit de la deuxième loi de Newton. Elle s'énonce ainsi :

Soit un corps de masse m constante, l'accélération subie par un corps dans un référentiel galiléen est proportionnelle à la résultante des forces qu'il subit, et inversement proportionnelle à sa masse m.

Ceci est souvent récapitulé dans l'équation :

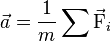
— ou —

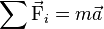
où

• désigne les forces extérieures exercées sur l'objet,
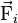
• m est sa masse, et
• correspond à l'accélération de son centre d'inertie G.

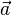
Ainsi, la force nécessaire pour accélérer un objet est le produit de sa masse et de son accélération : plus la masse d'un objet est grande, plus grande est la force requise pour l'accélérer à une vitesse déterminée (en un laps de temps fixé). Quelle que soit la masse d'un objet, toute force nette non-nulle qui lui est appliquée produit une accélération.

Théorème de la quantité de mouvement

Une forme plus générale du PFD, valable également si la masse change au cours du temps est

La force est égale aux changements de quantité de mouvement par unité de temps.

Ceci est souvent récapitulé dans l'équation :

où

• désigne les forces exercées sur l'objet,
• est la quantité de mouvement, égale au produit de sa masse m et de sa vitesse .

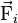
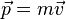
Ce théorème est appelé théorème de la quantité de mouvement. Pour un solide de masse fixe en mécanique newtonienne, il est équivalent à la deuxième loi de Newton.

Cette forme est intéressante dans le cas où la masse n'est pas constante, comme par exemple dans le cas de la propulsion par réaction.

Principe de d'Alembert

On peut aussi écrire le PFD sous la forme :

.

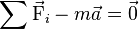
Cela permet une traduction graphique du PFD (voir l'article Statique graphique) : si l'on met les vecteurs forces bout à bout, on obtient un polygone ouvert (puisque la somme des forces est non nulle) ; le vecteur est le vecteur qui ferme le polygone.

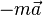
On retrouve cette forme en se plaçant dans le référentiel de l'objet étudié : si l'accélération est non nulle, le référentiel n'est plus galiléen (voir ), on introduit donc la force d'inertie

et l'on retrouve le principe fondamental de la statique (le solide étant immobile dans son propre référentiel)

.

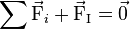
L'écriture du PFD sous cette forme facilite la résolution de certains problèmes.

Ceci constitue un cas particulier du principe de d'Alembert : puisque

,

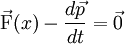
a fortiori

.

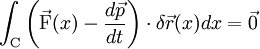
Dynamique avec les torseurs

On peut résumer le PFD en translation et en rotation avec les torseurs d'action et dynamique :

.

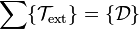
Principe fondamental de la dynamique en rotation

En mécanique du solide, on considère également la rotation d'un solide. Le principe fondamental de la dynamique comporte alors un « volet » sur la rotation :

Soit un corps de moment d'inertie par rapport à son centre de gravité J_G constant, l'accélération angulaire subie par un corps dans un référentiel galiléen est proportionnelle à la résultante des moments des forces qu'il subit, et inversement proportionnelle à son moment d'inertie.

Ceci est souvent récapitulé dans l'équation, pour un axe de rotation passant par G :

,

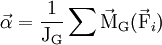
— ou —

,

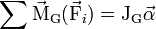
— ou encore —

.