Rapport anharmonique - Définition

Rapport anharmonique sur un cercle

La propriété du birapport des sinus a une conséquence pour 6 points cocycliques ABCDMP. Les angles et étant égaux ou supplémentaires, leurs sinus sont égaux. Le birapport des droites M(ABCD) est égal à celui des droites P(ABCD). En conséquence on peut parler du birapport de 4 points sur un cercle. On démontre, sans les sinus, en géométrie projective que cette propriété est vraie pour une conique quelconque (étant donnée une conique, si ABCDM sont fixes et si P parcourt la conique, alors le birapport des droites P(ABCD) est constant).

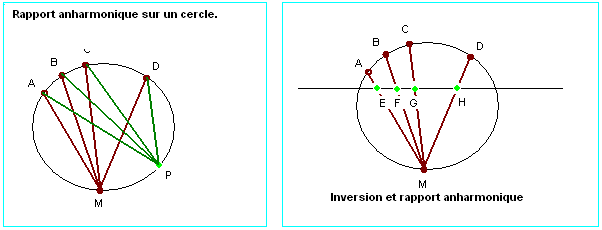
On peut en déduire que l'inversion de 4 points alignés, EFGH, de centre M, conserve leur birapport sur leurs images cocycliques ABCD.

Complexes

Déf : Soient α,β,γ,δ des complexes deux à deux distincts. On définit leur birraport : .
Prop : Quatre points (d'affixe) α,β,γ,δ sont cocycliques ou alignés ssi [ .

Prop : Il existe une relation de Chasles multiplicative dans l'ensemble des rapports anharmoniques mettant en jeu cinq nombres a, b, c, d et e. . Les nombres a et b ne changent pas, le nombre d sert d'intermédiaire entre c et e. Un simple développement de l'expression permet de la vérifier.