Géométrie projective - Définition

Introduction

En mathématiques, la géométrie projective est le domaine de la géométrie qui modélise les notions intuitives de perspective et d'horizon. Elle étudie les propriétés des figures inchangées par projection.

Considérations historiques

La géométrie projective trouve ses origines dans le travail de Pappus d'Alexandrie (IV^e siècle après Jésus-Christ) qui introduit le rapport anharmonique et fait référence à un travail d'Apollonius de Perga.

Elle a ensuite été étudiée au XVII^e siècle par des mathématiciens comme Pascal ou des architectes comme Desargues au XVII^e siècle, puis théorisée et enseignée à la fin du XVIII^e siècle par Gaspard Monge qui l'enseignera à l'école polytechnique.

Poncelet, dans son Traité des propriétés géométriques des figures lui donne un véritable essor en partant de considérations de géométrie pure. En effet la géométrie affine n'aurait pas permis cette découverte puisqu'elle interdisait l'intersection des droites parallèles, notion essentielle en géométrie projective.

Par suite la géométrie pure va fortement prédominer pendant tout le XIX^e siècle siècle jusqu'à ce que des méthodes analytiques soient enfin découvertes par August Ferdinand Möbius et Julius Plücker. Mais c'est Felix Klein qui, à la fin du XIX^e siècle, clarifie le lien entre géométrie projective et géométrie euclidienne.

C'est aussi à la même époque qu'eut lieu une évolution conceptuelle majeure ; auparavant la géométrie était la science des figures, les géomètres du tournant du siècle se concentrèrent sur les transformations desdites figures, les lois de composition internes des diverses transformations, la structure de certains groupes de transformations (questions de la commutativité, de l'associativité, de la transformation inverse, etc.), les invariants de telle ou telle famille de transformations, les axiomes minimaux permettant ces propriétés de transformations.

La géométrie projective est aujourd'hui largement utilisée par les systèmes de vision par ordinateur et de rendu graphique (tels que OpenGL).

Espace projectif

Un espace projectif est défini en mathématiques comme l'ensemble des droites vectorielles d'un espace vectoriel ; on peut imaginer l'œil d'un observateur placé sur l'origine d'un espace vectoriel, et chaque élément de l'espace projectif correspond à une direction de son regard.

Un espace projectif se démarque d'un espace vectoriel par son homogénéité : on ne peut distinguer en son sein aucun point particulier comme l'origine d'un espace vectoriel. En cela il se rapproche d'un espace affine.

Définition vectorielle

Soit un K-espace vectoriel (K est un corps, en général ou ), non réduit à {0}. On définit sur la relation d'équivalence suivante :

.

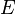
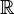
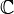
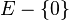
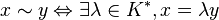
Alors on appelle espace projectif sur l'ensemble quotient de par la relation d'équivalence  : .

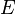
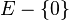
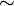
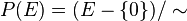
Pour chaque élément de on notera sa classe d'équivalence : . On a donc : si et seulement si et sont colinéaires.

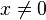
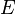
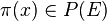
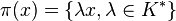
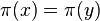
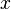
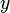
L'application est appelée projection canonique.

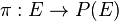
Plus simplement l'espace projectif est l'ensemble des droites vectorielles de  ; l'élément de l'espace projectif est la droite vectorielle de dont un vecteur directeur est .

Si est de dimension finie alors on dit que est de dimension finie et on note la dimension de l'espace projectif. En particulier :

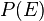
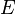
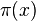
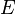
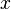
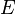
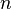
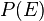
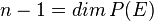
• Si n=1 alors est un singleton (dimension nulle) ;
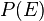
• Si n=2 alors est un plan vectoriel et est appelé droite projective.
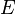
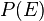
• Si n=3 alors est appelé plan projectif ; c'est le cadre le plus courant pour faire de la géométrie.

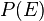
Si l'espace est l'espace vectoriel de dimension « typique », c'est-à-dire alors on a une notation particulière pour l'espace projectif : au lieu de .

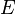
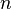
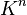
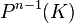
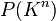
Définition affine

Espace projeté dans un plan projectif

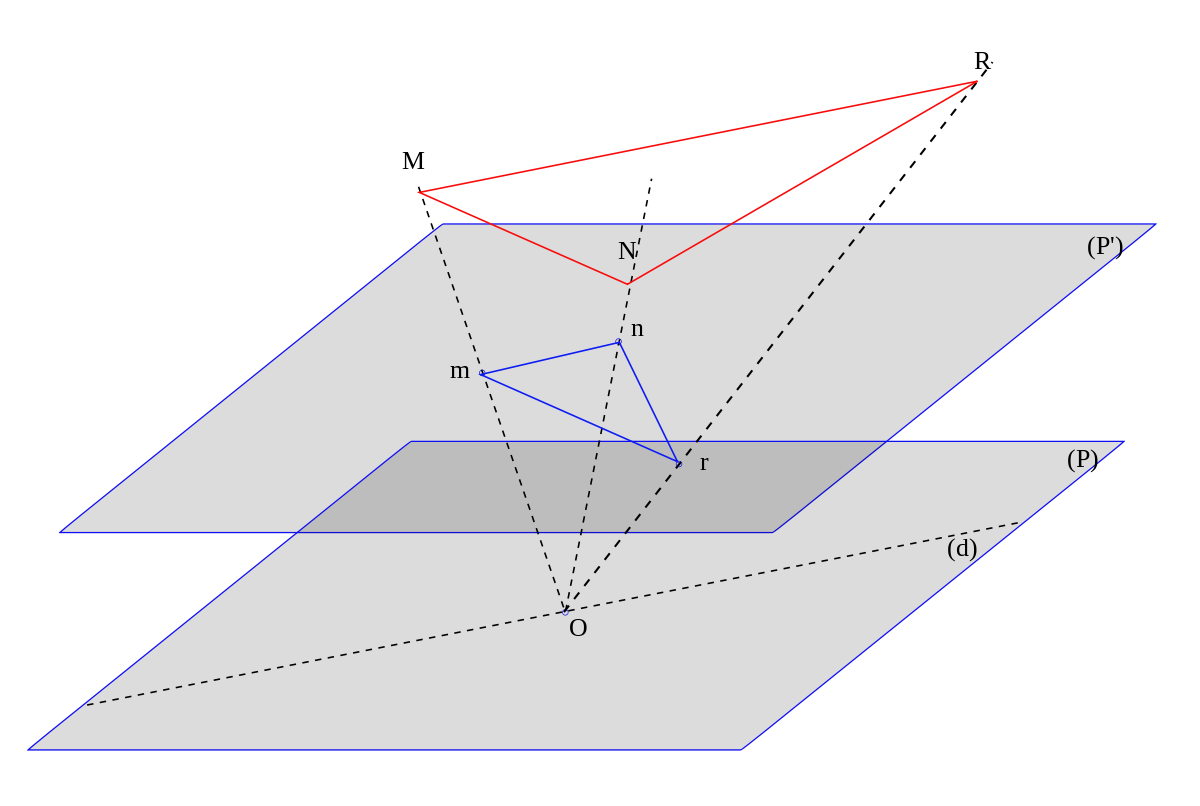
L'aspect formel de la définition vectorielle ne doit pas faire oublier que la notion d'espace projectif est née de la projection centrale et est, avant tout, une notion géométrique. Pour prendre l'exemple de l'espace projectif de , on peut observer le dessin ci-contre où les points m, n et r appartiennent au plan (P'). Il faut imaginer un observateur placé en O. Cet observateur voit tous les points de la droite (OM) en m , ceux de la droite (OR) en r et ceux de la droite (ON) en n. les droites (d) du plan (P) ne sont pas vues comme des points de (P'). Il y a donc bijection entre les droites vectorielles de non parallèles à (P) et les points du plan (P').

L'espace projectif de est donc en bijection avec le plan affine (P') auquel on ajoute l'ensemble des droites vectorielles de (P). Un plan projectif est donc constitué d'un plan affine (P') qui contient l'ensemble des points propres de auquel on adjoint toutes les droites vectorielles (ou directions) de (P'). Chaque point du deuxième ensemble s'appelle point impropre de ou point à l'infini.

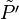
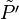
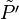
Cette notion permet, par exemple, de parler, dans un plan, d'intersection entre deux droites quelconques : les droites seront sécantes en un point propre de (P') ou bien en un point impropre dans le cas où les droites sont parallèles.

Cette notion se généralise à tout espace projectif de dimension n : c'est un espace affine (P) de dimension n auquel on adjoint l'ensemble des directions de (P).

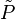
En particulier, si (P) = K, la droite projective associée est l'ensemble où est un point extérieur à , prolongeant les opérations algébriques de la manière suivante :

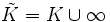
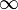
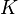
• pour tout x de K,
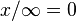
• pour tout x de K ^* ,

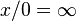
Cette double relation, d'une part avec un espace vectoriel quotienté, d'autre part avec un espace affine complété fait la richesse de l'étude de la géométrie projective. De même, ce double aspect sera important à conserver quand il s'agira de donner des coordonnées aux points de l'espace projectif.

Définition de l'espace affine

Inversement, par l'introduction des éléments impropres (un plan impropre, en l'occurrence), Desargues a montré que l'espace affine s'inscrit dans l'espace projectif. La définition de l'espace affine est fort simple, puisqu'elle consiste en l'élimination de ces éléments impropres.