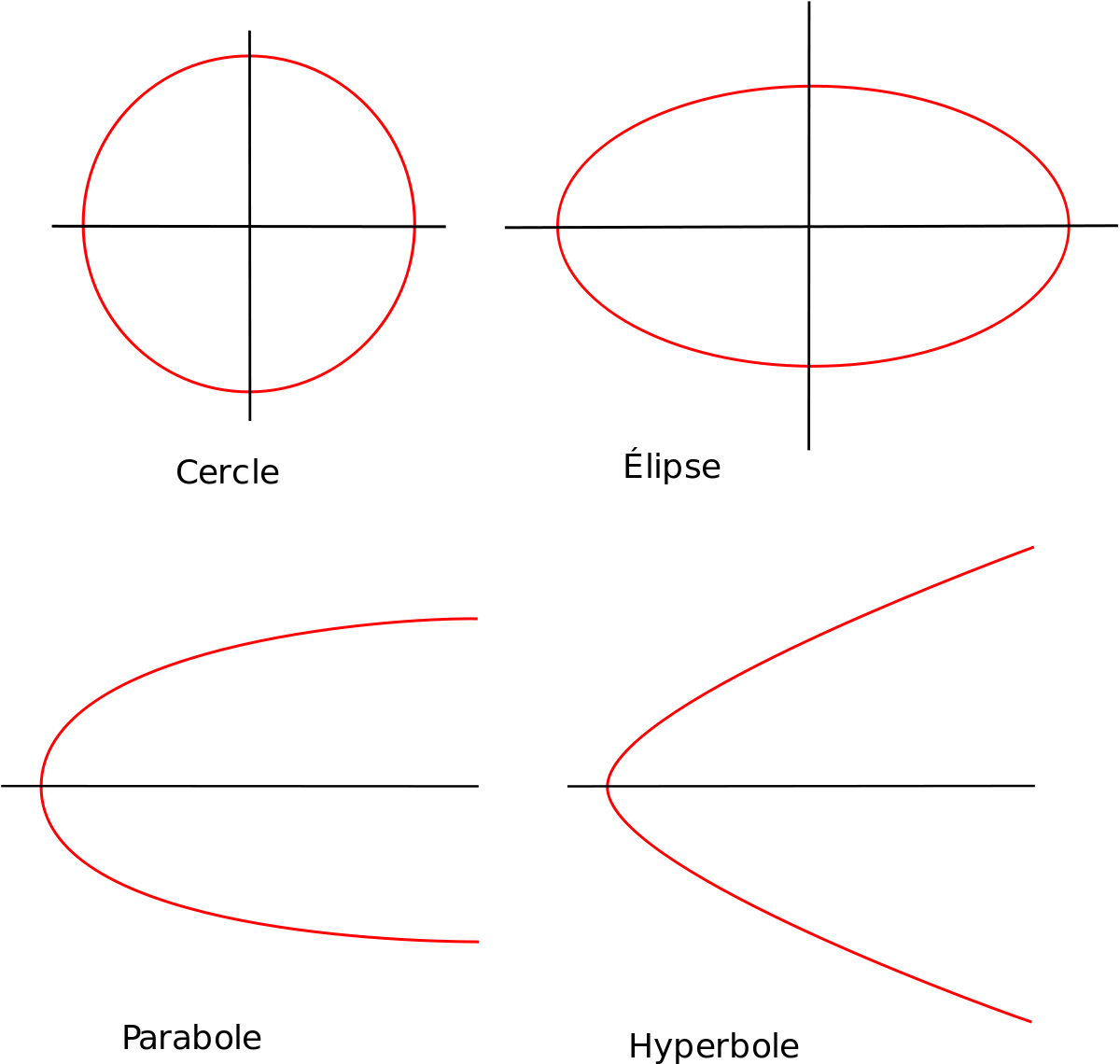Conique - Définition

Introduction

Les coniques constituent une famille très utilisée de courbes planes algébriques, qui peuvent être définies de plusieurs manières différentes, toutes équivalentes entre elles.

Définition purement géométrique euclidienne

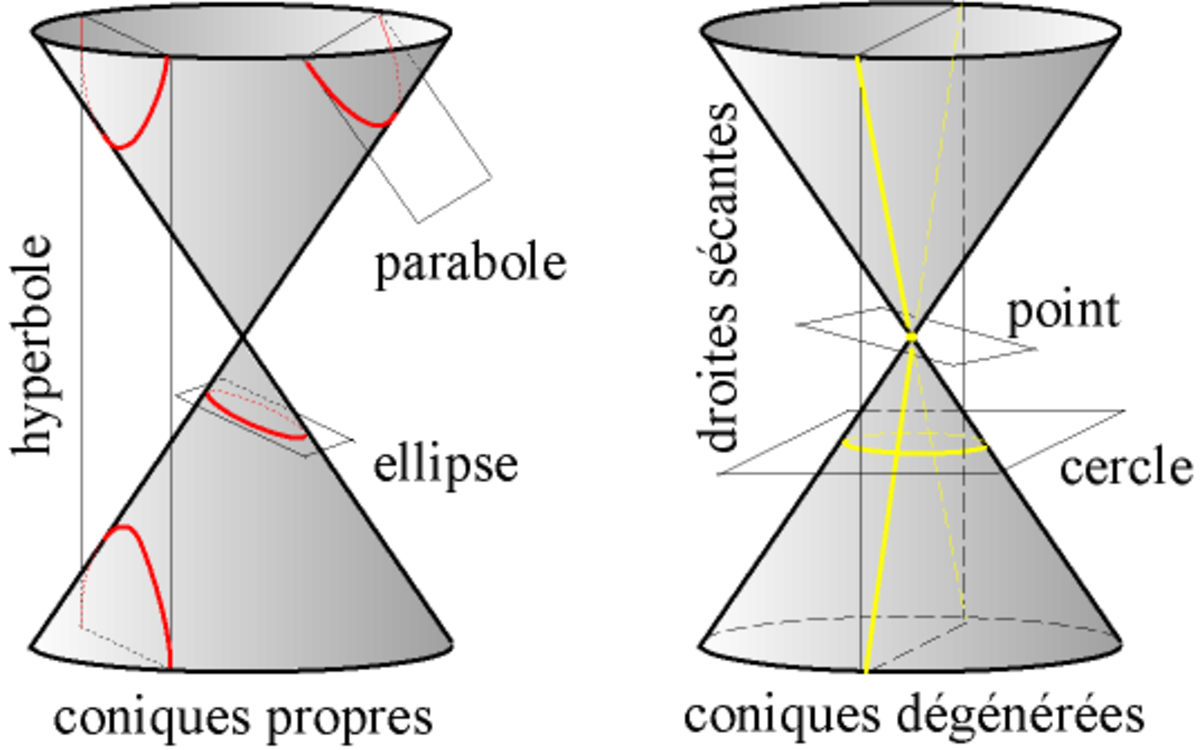
Les coniques forment une famille de courbes planes résultant de l'intersection d'un plan avec un cône de révolution.

Intersection d'un plan et d'un cône de révolution

Selon les positions relatives du plan et du cône, on obtient différents types de coniques :

• les coniques propres, quand le plan n'est pas perpendiculaire à l'axe du cône, et ne passe pas par son sommet. On distingue trois sortes de coniques propres en fonction de l'angle d'inclinaison du plan avec l'axe du cône :
  • si cet angle est supérieur à l'angle d'ouverture du cône, l'intersection est une ellipse;
  • si l'angle d'inclinaison est inférieur à l'angle d'ouverture, c'est une hyperbole;
  • et si les deux angles sont égaux, c'est une parabole.
• les coniques partiellement dégénérées :
  • l'intersection est un cercle quand le plan est perpendiculaire à l'axe du cône;
  • l'intersection est une hyperbole équilatère quand l'angle d'inclinaison du plan est inférieur de 45° à l'angle d'ouverture du cône;
• et les coniques totalement dégénérées, quand le plan contient le sommet du cône :
  • l'intersection est un couple de droites sécantes, si l'angle d'inclinaison du plan avec l'axe du cône est inférieur à l'angle d'ouverture du cône ;
  • l'intersection est réduite à une droite si ces angles sont égaux.
  • enfin elle est réduite à un point si l'angle d'inclinaison est supérieur à l'angle d'ouverture.

Définition monofocale

La définition monofocale des coniques est encore appelée définition par foyer et directrice de ces coniques.

Définition

Quatre coniques ayant même foyer et même directrice

Dans un plan (p), on considère une droite (D) et un point F non situé sur (D). Soit e un réel strictement positif.

On appelle conique de droite directrice (D), de foyer F et d'excentricité e l'ensemble des points M du plan (p) vérifiant :

où

d(M,F) mesure la distance du point M au point F

et

d(M,(D)) mesure la distance du point M à la droite (D)

Les ellipses sont des courbes fermées et bornées ; les paraboles sont ouvertes et infinies ; les hyperboles possèdent deux branches symétriques par rapport au point d'intersection de leurs asymptotes communes.

Mise en équation

Soit O la projection orthogonale du point F sur la droite (D). Dans le plan (p) on définit alors le repère orthogonal (O, (OF), (D)).

Soit p la distance de O à F (ep s'appelle le paramètre). Dans le repère défini précédemment F a pour coordonnées (p,0).

Pour un point M de coordonnées (x,y) on peut exprimer les distances précédentes à l'aide des deux formules suivantes :

ce qui implique en élevant [1] au carré et en utilisant [2] et [3] :

soit après simplification :

types de conique

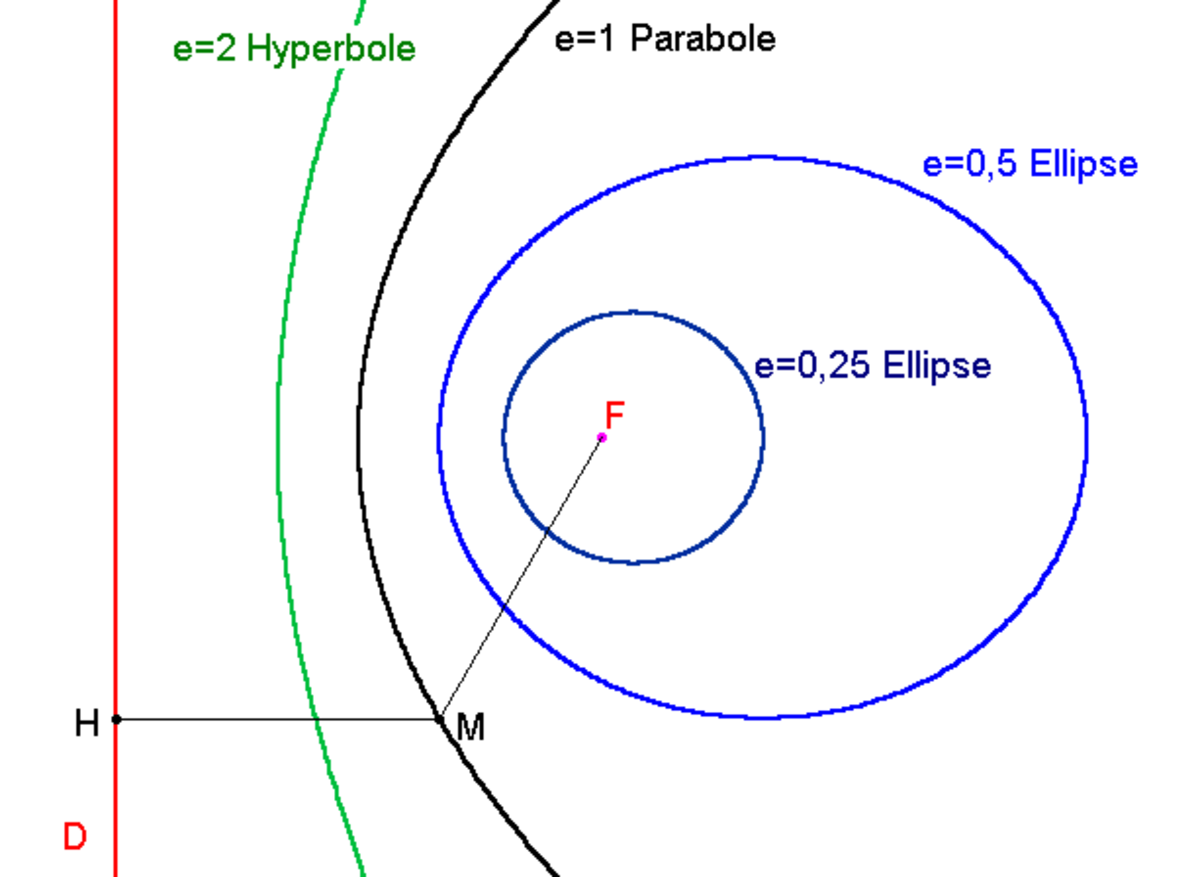
En fonction des valeurs de e on obtient plusieurs types de courbes :

• Si 0 < e < 1 une ellipse
• Si e = 1 une parabole
• Si e > 1 une hyperbole

Il est possible de déterminer la nature de la conique avec la matrice de la forme quadratique :

• Si detM > 0 un genre ellipse
• Si detM = 0 un genre parabole
• Si detM < 0 un genre hyperbole

Les coniques dégénérées s'obtiennent en modifiant les conditions précédentes

• Si F est sur (D), on obtient :
  • Si e < 1 le point O (qui est aussi le point F);
  • Si e = 1 la droite perpendiculaire à (D) passant par F;
  • Si e > 1 deux droites sécantes ;
• Si e = 0, le point O (qui est aussi le point F).

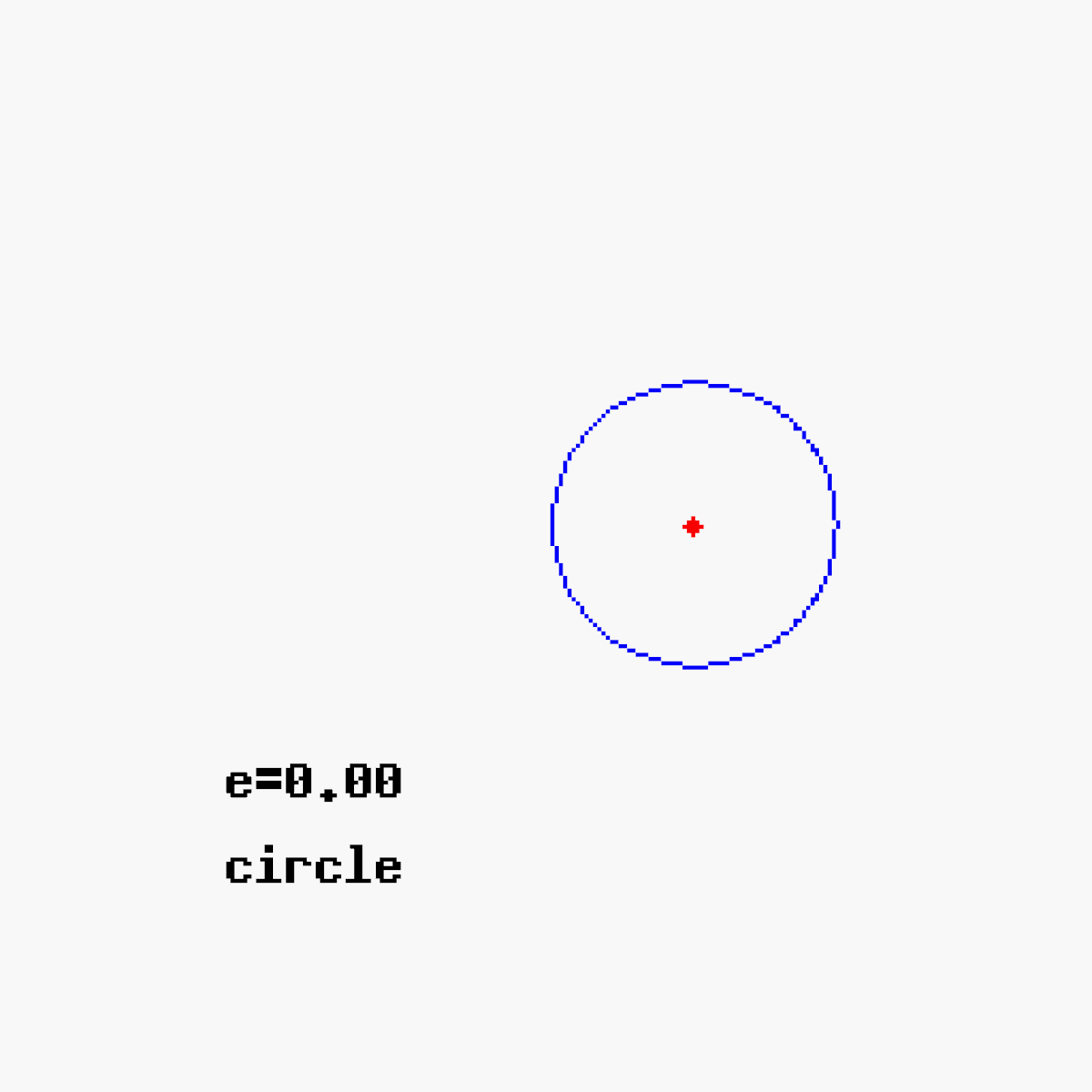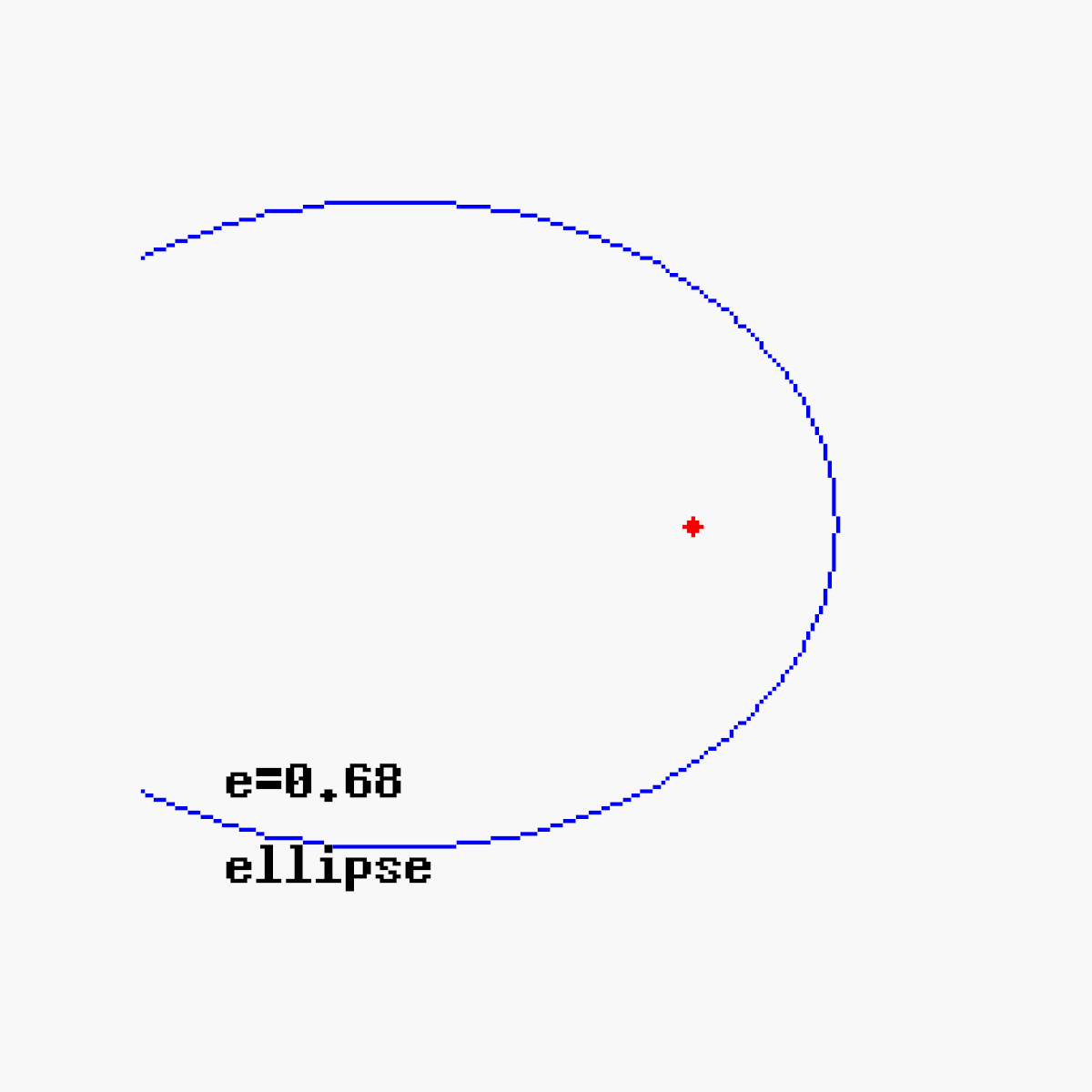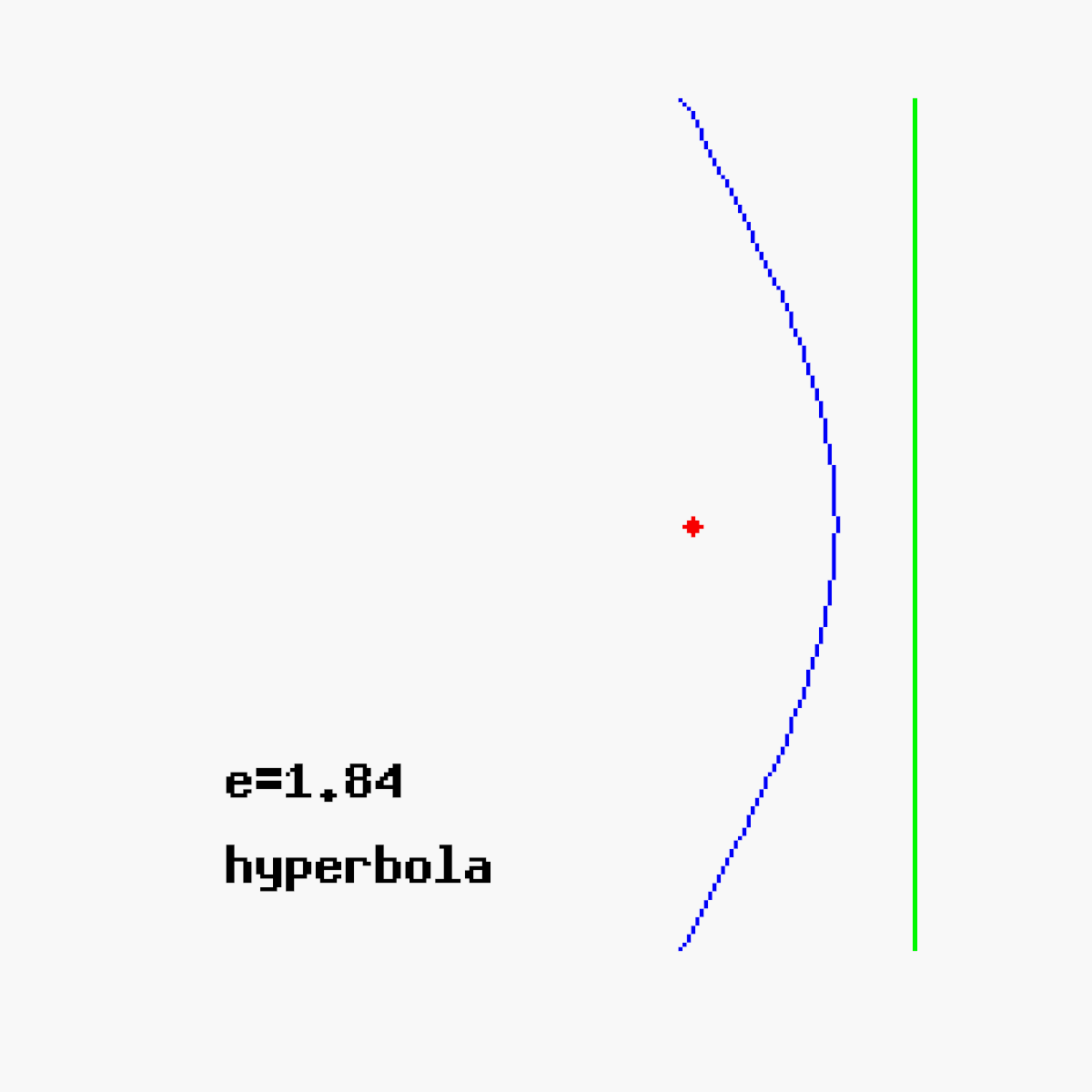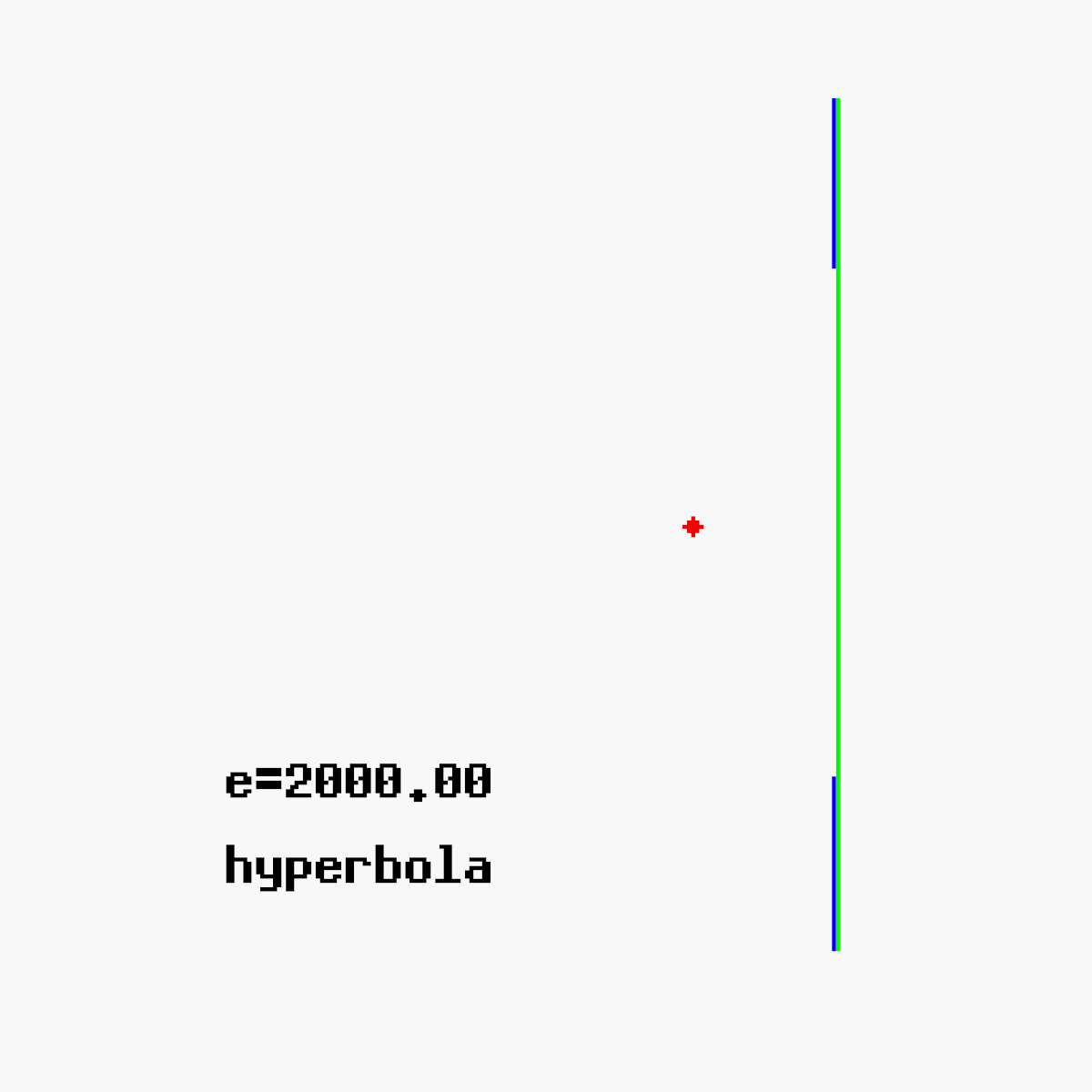
Il n'existe donc pas de définition de cercle par foyer et directrice. En revanche, si pe = r et si e tend vers 0 (ce qui augmente à l'infini la distance entre le foyer et la directrice), l'ellipse se rapproche d'un cercle de centre F et de rayon r