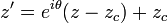Rotation plane - Définition

Expression complexe

La rotation de centre C et d'angle θ a pour expression complexe

c’est-à-dire que, si z_c est l'affixe de C, le point M d'affixe z a pour image le point M' d'affixe z' vérifiant l'égalité précédente.

Réciproquement, toute transformation dont l'expression complexe est

z' = az + b, où a et b sont des complexes, vérifiant |a| = 1 et a ≠ 1

est une rotation dont le centre C a pour affixe et dont l'angle est l'argument de a

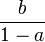
Cette écriture complexe permet de retrouver aisément toutes les propriétés précédentes.