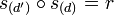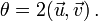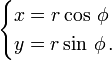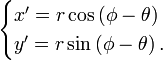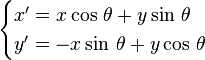Rotation plane - Définition
La liste des auteurs de cet article est disponible ici.
Composition et décomposition
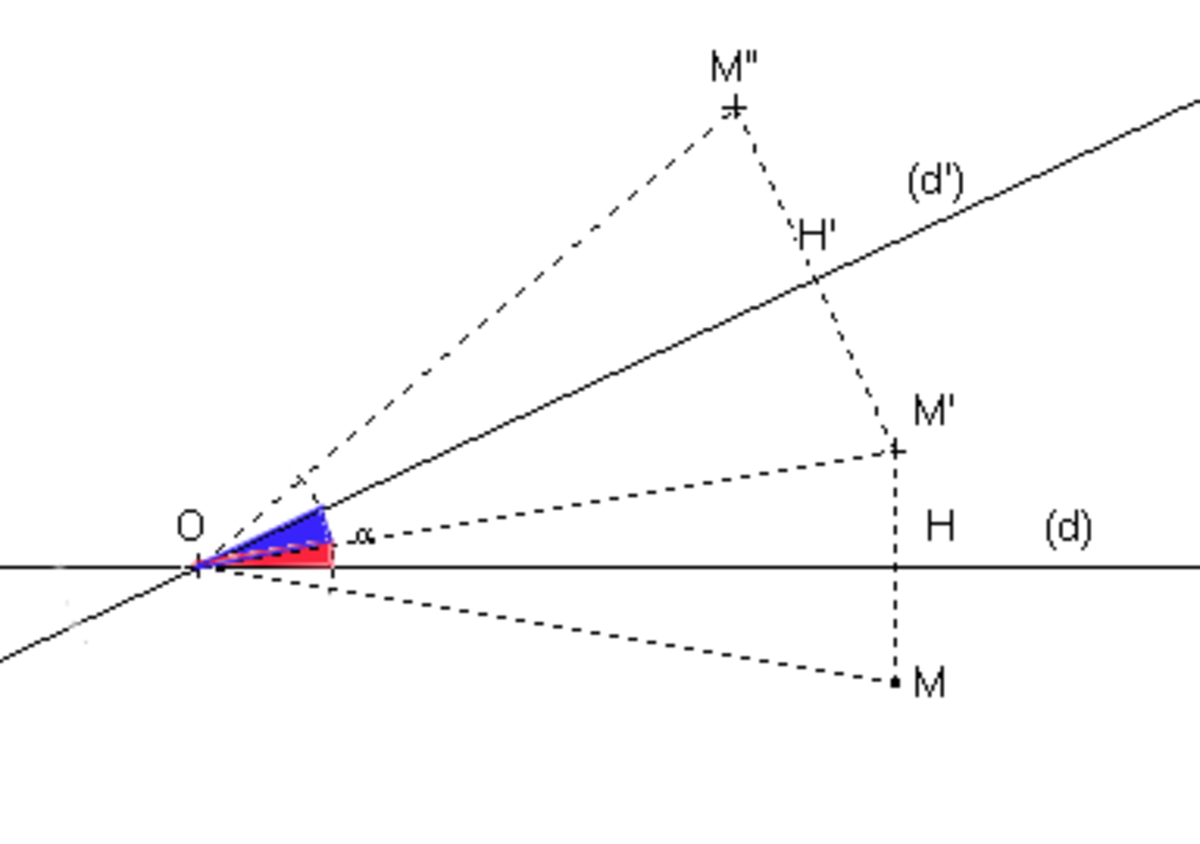
La composée de deux réflexions (ou symétries) s et s d'axes sécants en O est une rotation de centre O . Plus précisément, si
-
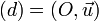
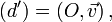
alors
où r est une rotation de centre O et d'angle θ
Réciproquement, toute rotation de centre C se décompose en deux réflexions (symétries) d'axes sécants en C dont l'un peut être choisi arbitrairement pourvu que l'autre permette, en multipliant par deux l'angle formé par les vecteurs directeurs, de retrouver l'angle de la rotation.
La composée de deux rotations de même centre C et d'angles θ et θ' est une rotation de centre C et d'angle θ + θ'. Ces deux rotations commutent, c’est-à-dire que
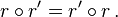
L'ensemble des rotations de centre C, muni de la loi de composition est donc un groupe commutatif isomorphe à
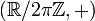
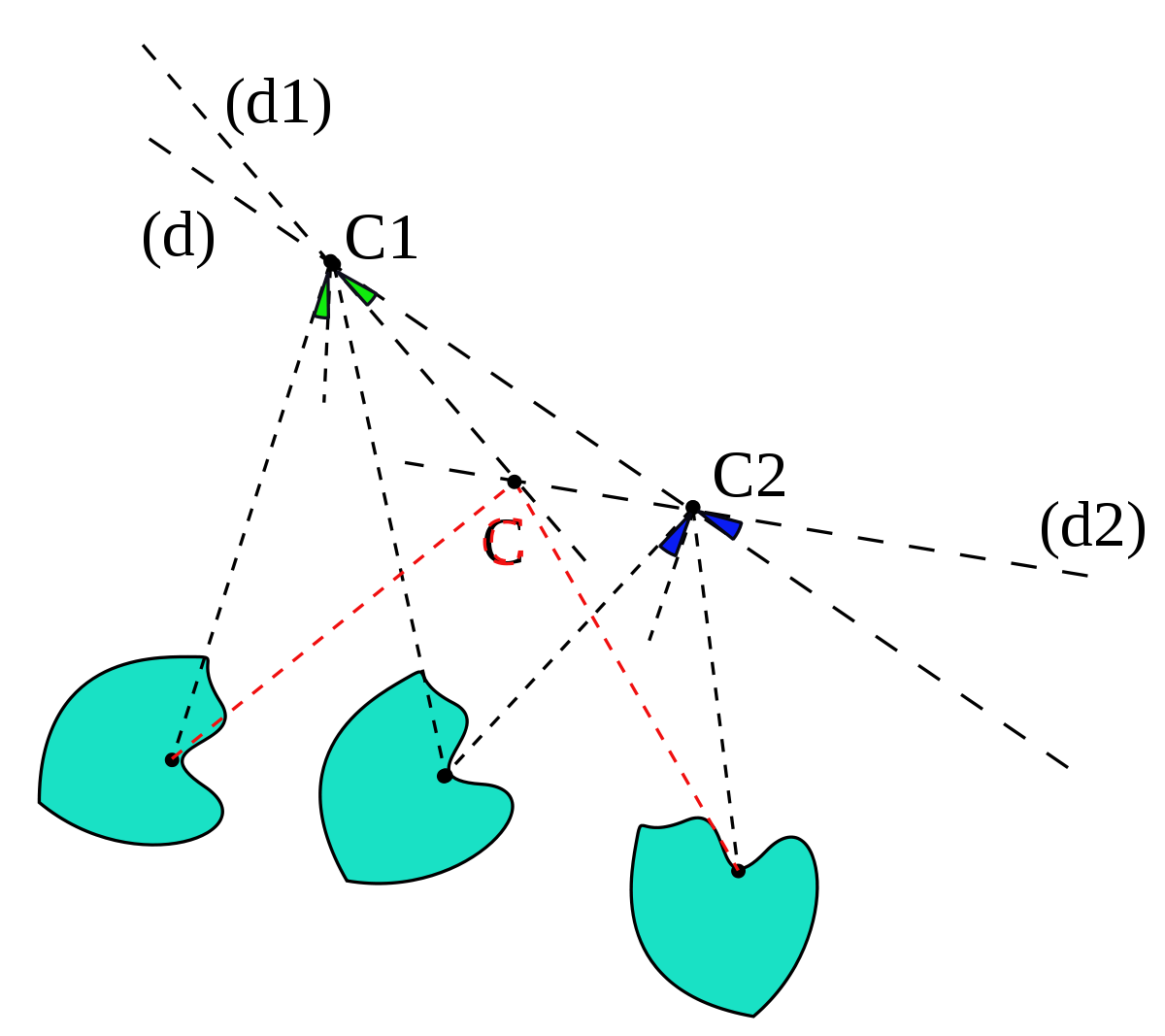
La composée de deux rotations de centres différents et d'angles θ et θ' est
- une rotation d'angle θ + θ' si θ + θ' ≠ 2kπ
- une translation sinon
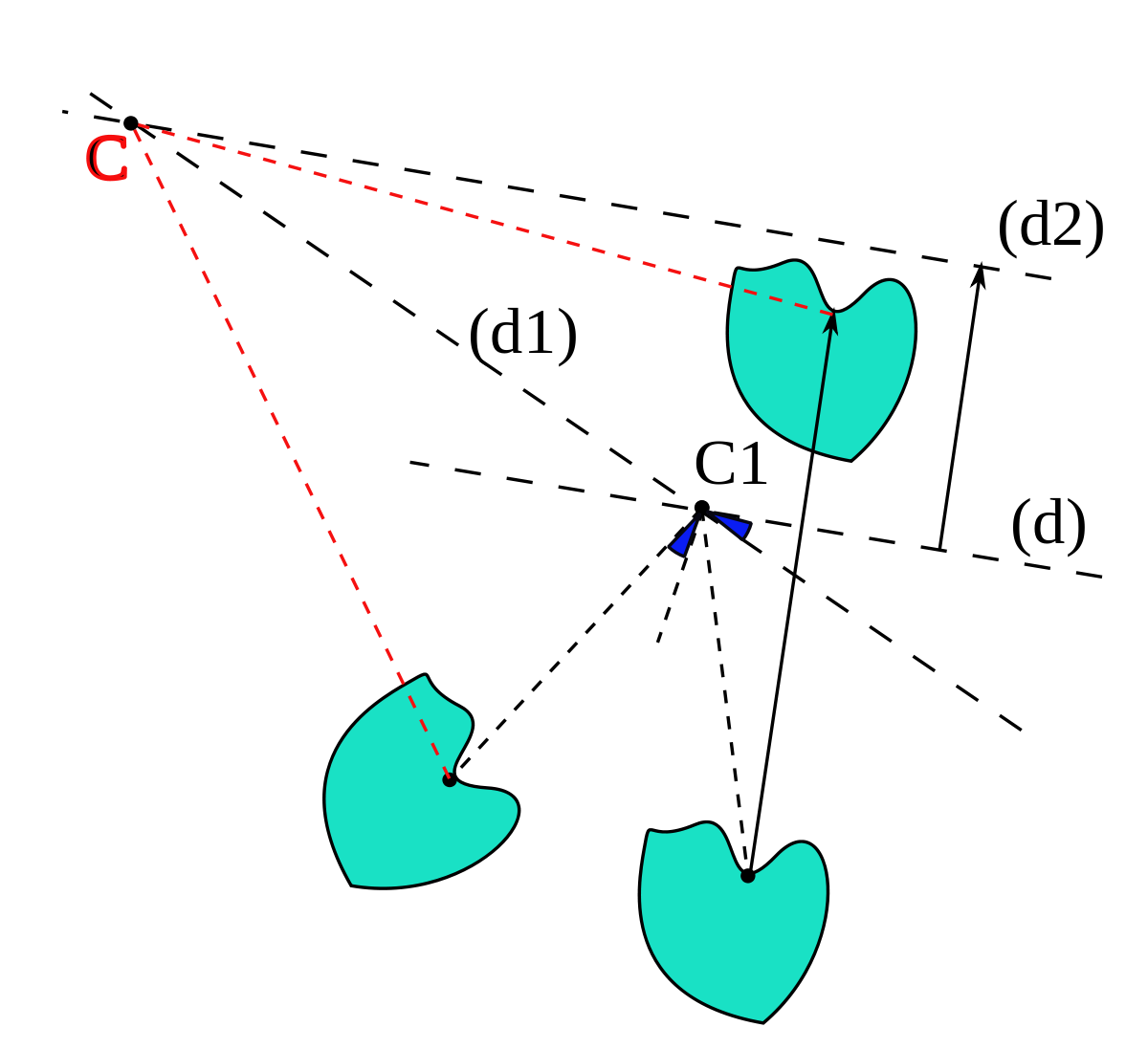
La recherche du nouveau centre et la démonstration de cette propriété s'obtient en décomposant chaque rotation en deux réflexions ayant un axe en commun. Cette composée est rarement commutative.
De plus, la composée d'une rotation et d'une translation reste une rotation de même angle dont le centre a changé.
Composée de deux rotations | 
Composée d'une rotation et d'une translation |
L'ensemble formé de toutes les rotations planes et de toutes les translations, muni de la loi de composition interne forme un groupe non commutatif appelé le groupe des isométries directes.
Invariance par rotation
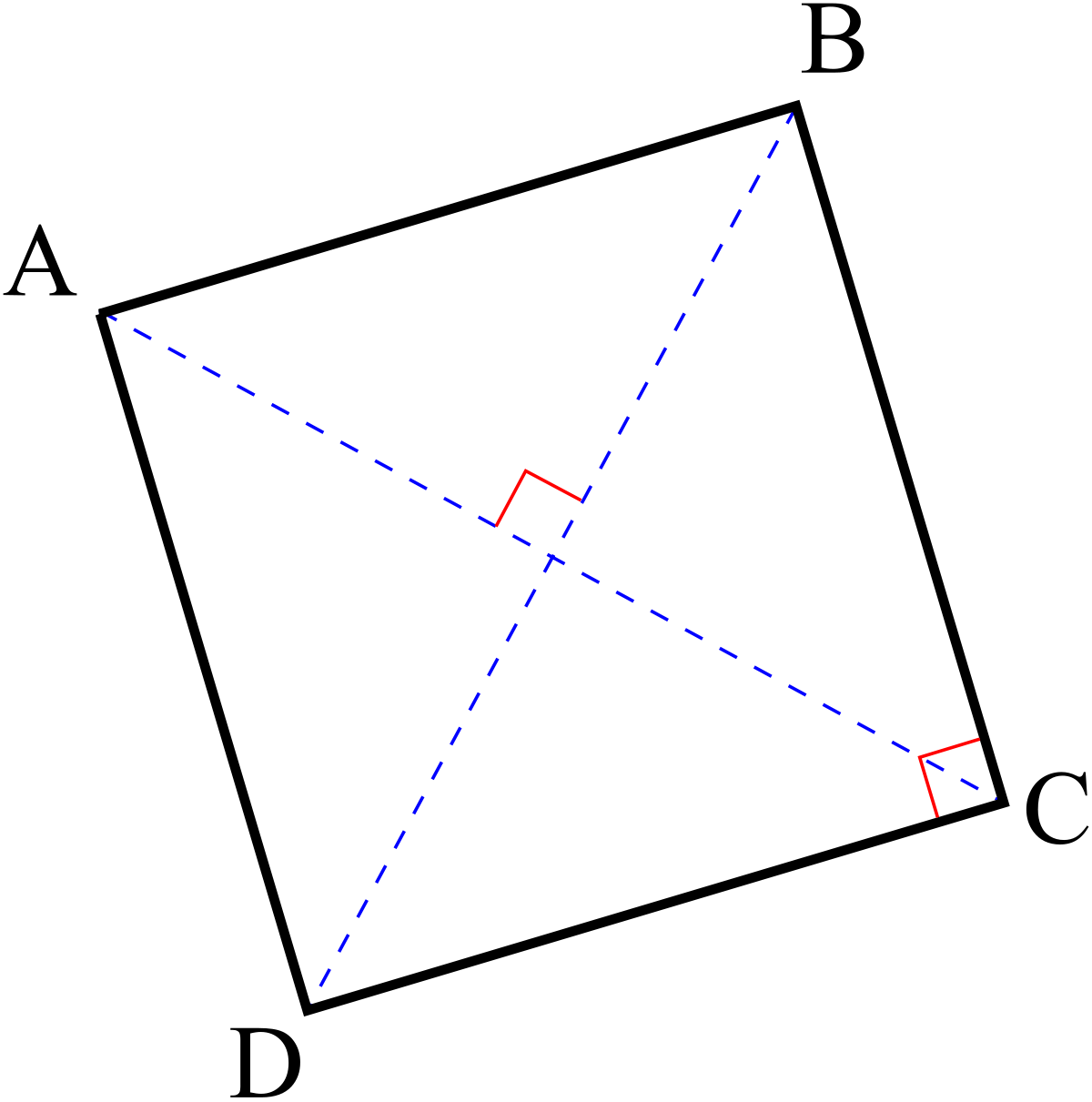
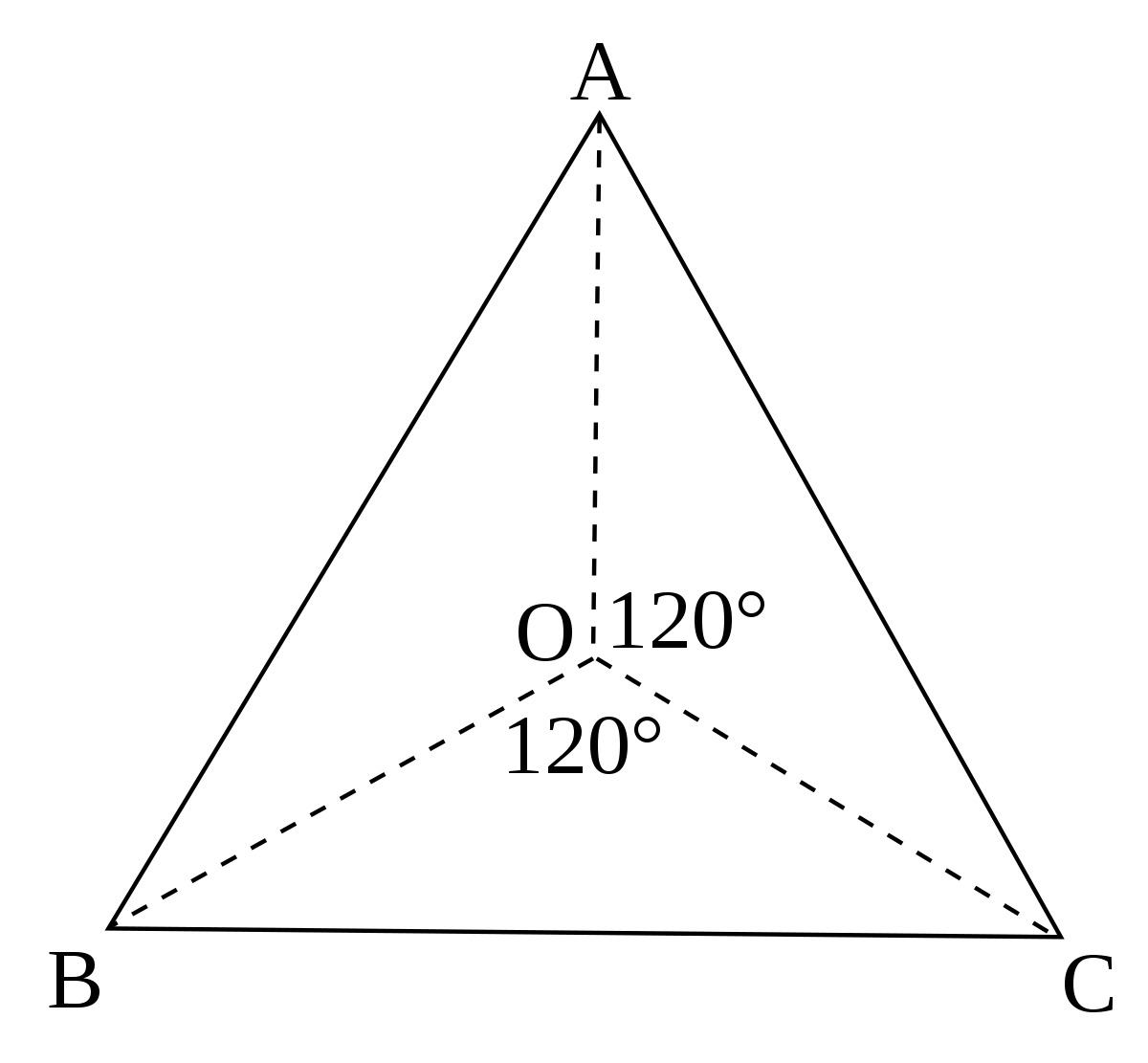
Certaines figures sont invariantes par rotation. C'est le cas par exemple du carré de centre O, invariant par rotation de centre O et d'angle droit ou plat, ou du triangle équilatéral de centre O invariant par rotation d'angle 120°. On dit alors que ces figures possèdent une symétrie d'ordre 4 (pour le carré) ou d'ordre 3 (pour le triangle). L'ordre de la rotation correspond au nombre de rotations nécessaires pour revenir au point de départ.
Carré et centre de rotation | 
Triangle équilatéral et centre de rotation |
Un polygone régulier à n côtés possède une symétrie d'ordre n. Il existe des figures possédant une symétrie d'ordre n qui ne possèdent pas pour autant un axe ou un centre de symétrie. C'est le cas par exemple du Triskell qui possède une symétrie d'ordre trois (Rq: à cause de l'alternance noir/blanc, le Taijitu, symbole du Yin Yang ne possède pas la symétrie d'ordre deux qu'on pourrait lui prêter au premier abord).
Symbole Yin-Yang | 
Triskell |
Formules de changement d'axes de coordonnées
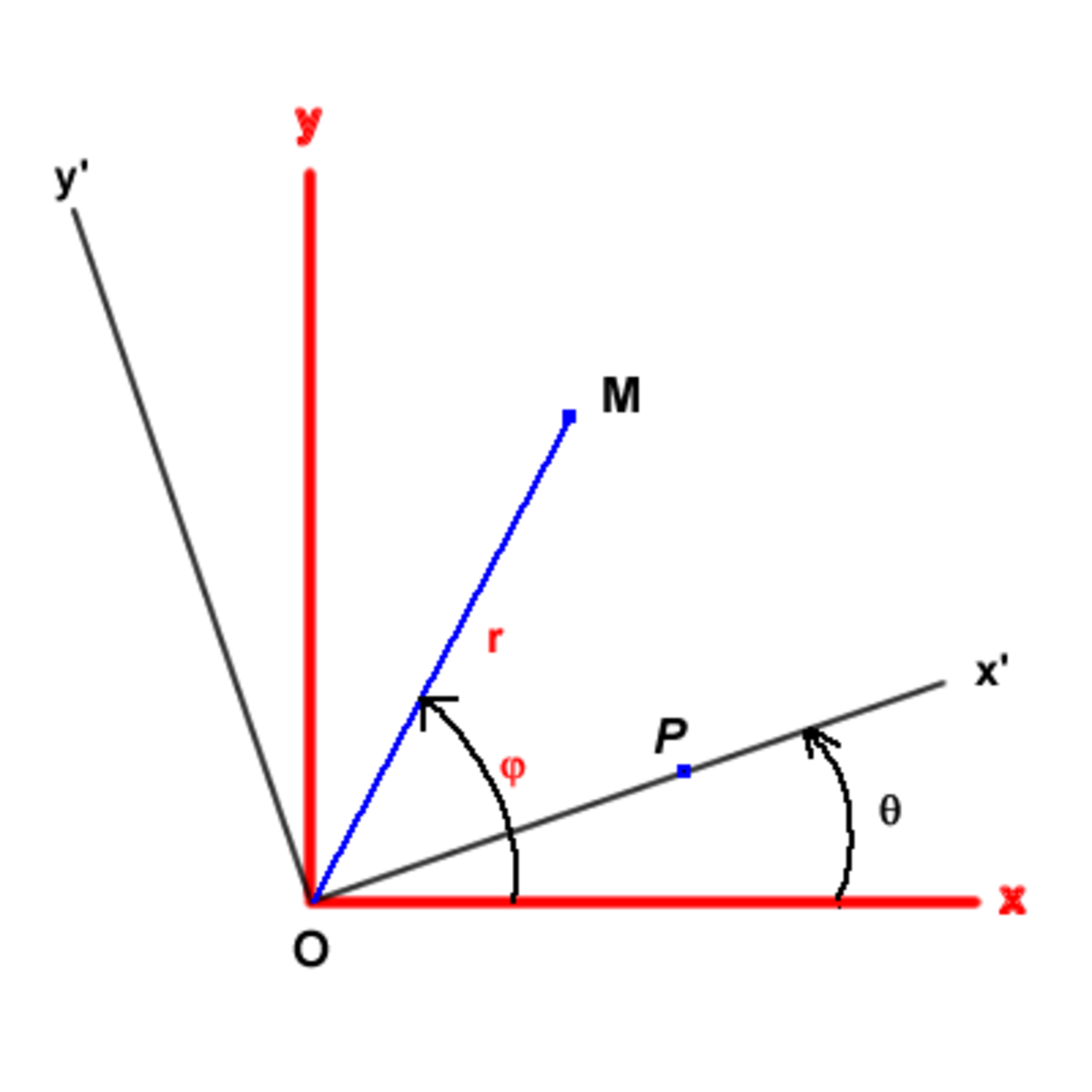
Il est courant en physique de devoir opérer une rotation des axes de coordonnées. Les formules qui suivent permettent d'exprimer les coordonnées d'un point M dans l'un des repères en fonction des coordonnées dans l'autre repère. Prenons un repère cartésien xOy dans lequel les coordonnées (x, y ) d'un point M s'expriment en fonction des coordonnées polaires (r, φ) par les formules élémentaires
Dans le nouveau repère x'Oy' déduit du précédent par une rotation d'angle θ (voir la figure) les nouvelles coordonnées polaires sont r et (φ - θ) et les coordonnées cartésiennes deviennent
En développant les fonctions trigonométriques et en tenant compte des expressions de x et y on arrive aux formules suivantes permettant de passer d'un repère à l'autre.
Un truc : s'il peut s'avérer difficile de mémoriser le signe à mettre devant sinθ (« + » dans une ligne et « - » dans l'autre) l'astuce consiste à considérer un point particulier (tel que P sur la figure) avec y = 0 ou y ’ = 0 selon les besoins et de vérifier alors sur la figure le signe de la coordonnée voulue.
