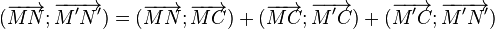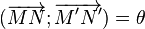Rotation plane - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Algèbre |
| Logique |
| Arithmétique |
| Probabilités |
| Statistiques |
En géométrie dans le plan, une rotation plane est une transformation qui fait tourner les figures autour d'un point et d'un certain angle. Cette transformation est une isométrie car les distances sont conservées. La figure n'a été ni déformée, ni agrandie.
La rotation fait intervenir la notion d'angle orienté ce qui fait d'elle une des transformations les moins évidentes des transformations euclidiennes.
Définition, propriétés et caractérisations
Définition
- Définition
- Dans le plan orienté, la rotation de centre C et d'angle θ est la transformation qui laisse C invariant et qui transforme tout point M distinct de C en le point M' tel que
- CM = CM' et
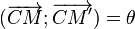
Les rotations les plus classiques sont
- les quarts de tour directs - rotations d'angle droit dans le sens trigonométrique (i.e. inverse des aiguilles d'une montre),
- les quarts de tours indirects - rotations d'angle droit dans le sens des aiguilles d'une montre,
- les rotations d'angle plat qui correspondent aux symétries centrales et aux homothéties de rapport -1,
- la rotation d'angle nul qui, quel que soit son centre, est l'identité.
- Construction de l'image d'un point par une rotation
- Tracer le cercle de centre C et de rayon [CM].
- Placer sur ce cercle le point M' , qui est l'image de M par cette rotation tel que
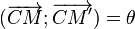
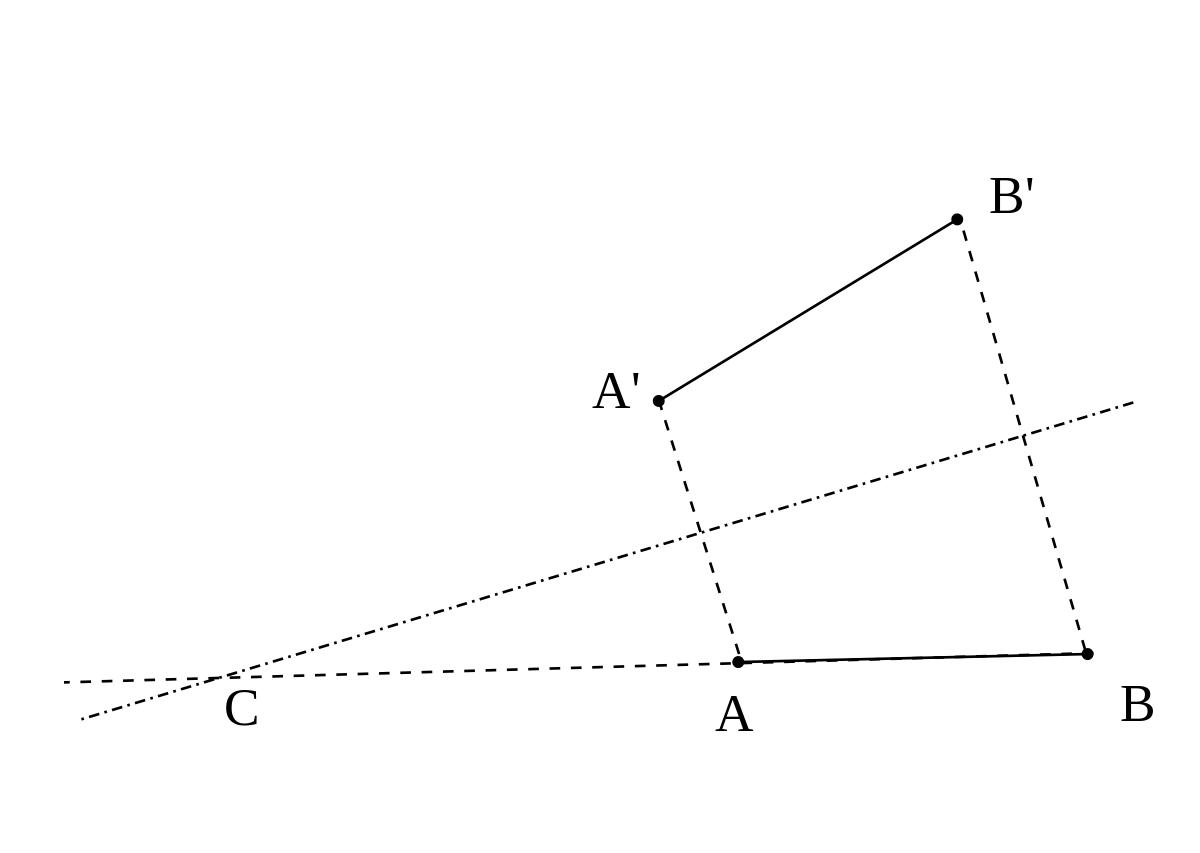
Une rotation peut aussi être déterminée par un centre et l'image d'un point : Si C est un point et A et A' deux points distincts de C tels que CA = CA', il existe une unique rotation de centre C et qui transforme A en A'. L'angle
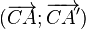
Propriétés
- Propriété 1
- L'image d'un segment [AB] est un segment [ A'B' ] tel que |AB| = |A'B'| .
- Propriété 2
- L'image d'un cercle C de centre O et de rayon r est un cercle C' de centre O' , l'image de O, et de même rayon r.
- Propriété 3 dite "de conservation"
- La rotation conserve :
- les longueurs ;
- les angles (l'image d'un angle est un angle de même amplitude) ;
- les parallèles (les images de deux droites parallèles sont deux droites parallèles) ;
- les aires (l'image d'une figure est une figure de même aire).
La rotation conserve donc les distances, c’est-à-dire que M'N' = MN. C'est donc une isométrie. Elle conserve donc les alignements, les angles et les concours. Elle conserve aussi l'orientation : si ABC est un triangle direct alors A'B'C' est aussi un triangle direct.
Fait important, on retrouve aussi l'angle de la rotation entre un vecteur et son image :
Les triangles CMN et CM'N' sont isométriques de même orientation car
- CM = CM'
- CN = CN'
-
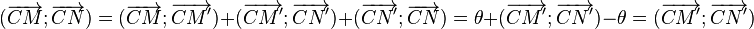
Donc, en particulier
- MN = M'N'
-
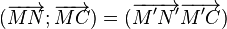
Une relation de Chasles sur les angles permet alors d'écrire :
les deux angles extrêmes s'annulent et celui du milieu vaut θ donc
Autre caractérisation
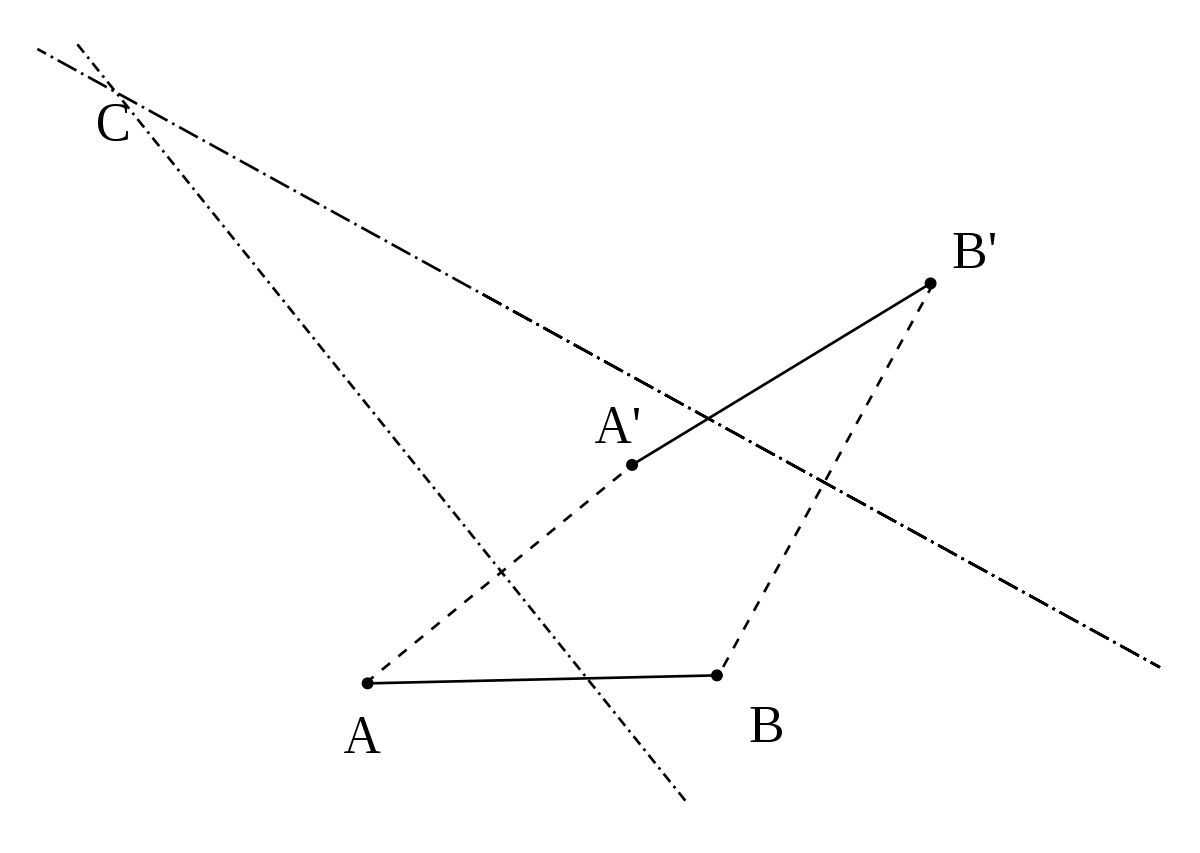
Une rotation peut donc être caractérisée par l'image de deux points : Soient A et B deux points distincts et A' B' deux points tels que AB = A'B' avec
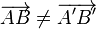
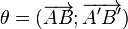
- AM = A'M'
-
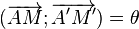
qui le définissent de manière univoque
Cas des médiatrices sécantes | 
Cas des médiatrices confondues |
Remarque : Si l'une des médiatrices n'existe pas, ce qui se produit quand A et A' ou B et B' sont confondus, le centre est alors immédiat : c'est, selon les cas, A ou B.
