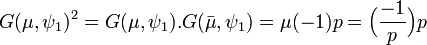Somme de Gauss - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
L'analyse harmonique permet de nombreux calculs sur les sommes de Gauss, ce paragraphe propose quelques exemples.
-
- Si m est un entier premier avec p, alors l'égalité suivante est vérifiée :
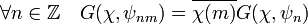
Ici Z désigne l'ensemble des entiers naturels et si z est un nombre complexe

-
- Si χ et ψ sont deux caractères différents du caractère constant égal à un, alors l'égalité suivante est vérifiée :
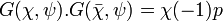
Cette propriété possède le corollaire suivant :
-
- Si μ désigne le caractère multiplicatif égal à 1 sur les carrés de Fp* et -1 sinon, alors l'égalité suivante est vérifiée :
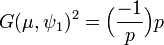
Dans cet article, (-1/p) désigne le symbole de Legendre.
-
- Si m est un entier premier avec p, alors l'égalité suivante est vérifiée :
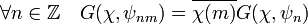
En effet, la définition d'une somme de Gauss implique les égalités suivantes :
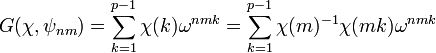
Utilisons le changement de variable suivant u = mk, on obtient :
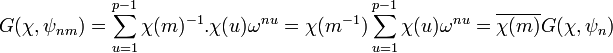
Ce qui termine la démonstration.
-
- Si χ et ψ sont deux caractères différents du caractère constant égal à un, alors l'égalité suivante est vérifiée :
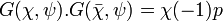
En effet, la définition d'une somme de Gauss implique les égalités suivantes :
![G(\chi, \psi).G(\bar \chi, \psi)=\sum_{k=1}^{p-1} \chi (k) \psi(k).\sum_{l=1}^{p-1} \overline{\chi (l)} \psi(l) = \sum_{k,l \in [1, p-1]} \chi(k\lambda_l) \psi(k)\psi(l) \;](https://static.techno-science.net/illustration/Definitions/autres/0/0432ffe81c27cd195f36329bc05224c3_c5da29dc3e7c9773c64a7d803f944eec.png)
Ici, λl désigne l'entier compris entre un et p - 1 tel que l.λl est congru à un modulo p. Utilisons le changement de variable suivant u = k.λl, on obtient :
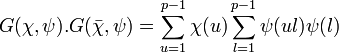
On remarque que l'application qui à la classe de l associe la valeur du caractère ψ pour la classe de ul est un caractère du groupe additif Fp. Si u est différent de l'unité, ce caractère est différent de ψ et donc lui est orthogonal car deux caractères distincts d'un groupe fini sont orthogonaux (cf caractère d'un groupe fini). On en déduit :
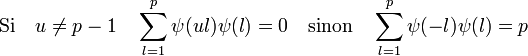
On en déduit, en limitant la somme à p - 1, les égalités suivantes :
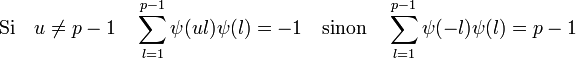
Ce qui démontre l'égalité suivante :
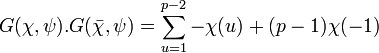
De même, le caractère multiplicatif χ est orthogonal au caractère constant égal à 1, en conséquence :
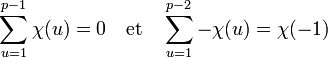
Ce qui démontre l'égalité suivante et termine la démonstration :
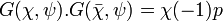
-
- Si μ désigne le caractère multiplicatif égal à 1 sur les carrés de Fp* et -1 sinon, alors l'égalité suivante est vérifiée :
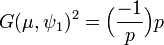
Comme μ est égal à son conjugué, la proposition précédente, montre que :