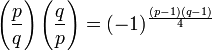Somme de Gauss - Définition

Introduction

En mathématiques, et plus précisément en arithmétique modulaire, la somme de Gauss est un nombre complexe.

La Somme de Gauss utilise les outils de l'analyse harmonique sur un groupe abélien fini sur le corps fini Z/pZ où p désigne un nombre premier impair et Z l'ensemble des entiers relatifs.

Elles sont introduites par le mathématicien Carl Friedrich Gauss qui les utilise dans ses Disquisitiones arithmeticae, parues en 1801.

Elles sont utilisées pour établir la théorie des polynômes cyclotomiques et possèdent de nombreuses applications. On peut citer par exemple une démonstration de la loi de réciprocité quadratique.

Définition

Dans cet article, p désigne un nombre premier impair, F_p le corps fini isomorphe à Z/pZ, F_p^* son groupe multiplicatif (c'est-à-dire le même ensemble sauf 0, avec la structure de groupe donnée par la multiplication) et ω désigne une racine primitive p-ième de l'unité, le caractère ψ_m désigne celui qui, à 1_F associe ω^m.

• Soit ψ un caractère du groupe additif (F_p, +) et χ un caractère du groupe multiplicatif (F_p^*, .), alors la somme de Gauss associée à χ et ψ est le nombre complexe, ici noté G(χ, ψ) et défini par :

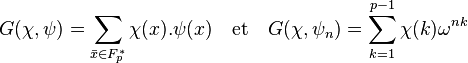
Pour une raison de simplicité, χ et ψ sont aussi considérés comme des fonctions définies sur Z l'anneau des entiers, avec la convention suivante :

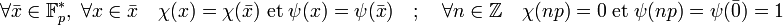
En termes de transformée de Fourier, on peut considérer l'application qui à χ associe comme la transformée de Fourier du prolongement de χ à F_p par l'égalité χ(0) = 0 dans le groupe additif du corps et l'application qui à ψ associe comme la transformée de Fourier de la restriction de ψ à F_p^* dans le groupe multiplicatif du corps.

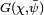
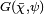
Applications

Somme quadratique de Gauss

L'exemple historique, publié par Gauss en 1801 est le suivant :

• Si τ_p est la somme définie à la ligne suivante, alors τ_p² est égal à (-1/p).p.

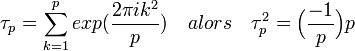
Soit H le sous-groupe du groupe multiplicatif F_p^* composé des résidus quadratiques de F_p^*. Soit P₁ la somme des caractères de ψ₁ sur H et P₂ la somme des caractères de ψ₁ sur le complémentaire de H dans F_p^*. L'égalité suivante est alors vérifiée :

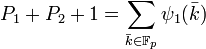
Or ψ₁ est un caractère additif différent du caractère constant sur F_p, il lui est donc orthogonal, on en déduit :

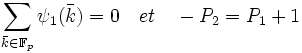
La valeur G(μ, ψ₁) de la dernière proposition du paragraphe précédent s'exprime de la manière suivante :

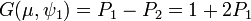
Enfin, l'application de F_p^* dans H qui à la classe de x associe la classe de x² est une application surjective telle que toute image admet exactement deux antécédents, en conséquence :

La dernière proposition du paragraphe précédent termine la démonstration.

 

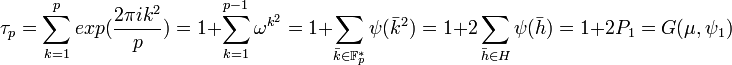
Loi de réciprocité quadratique

La loi s'exprime de la manière suivante si q est aussi un nombre premier impair distinct de p :

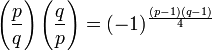
Elle se démontre à l'aide de la somme quadratique de Gauss et des propriétés des sommes.

Considérons l'anneau des entiers algébriques Z[ω]. Il contient τ_p, calculons alors τ_p^q modulo q dans Z[ω].

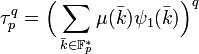
La formule du binôme de Newton, et les diviseurs des coefficients binomiaux montrent que :

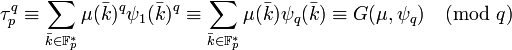
La première proposition décrite dans les propriétés des sommes de Gauss montre que :

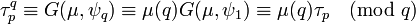
Les propriétés du symbole de Legendre montre aussi que :

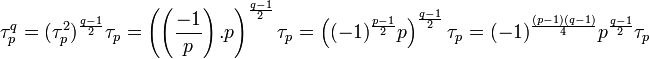
On en déduit l'égalité :

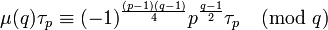
En multipliant par τ_p les deux termes de l'égalité et en divisant par p, on obtient :

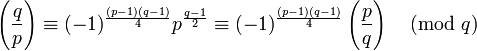
On remarque alors que l'égalité précédente est un produit de facteurs égaux à 1 ou -1, l'égalité précédente est donc aussi une égalité dans Z/qZ et aussi dans Z, on en déduit :

Ce qui termine la démonstration.