Groupe fini - Définition

Introduction

En mathématiques, un groupe fini est un groupe constitué d'un nombre fini d'éléments.

Introduction

Soit G un groupe. On note sa loi multiplicativement et 1 son élément neutre, sauf dans le cas où G est abélien, où la loi (resp. l'élément neutre) est notée additivement (respectivement 0).

On dit que G est un groupe fini lorsque l'ensemble G est fini. Le nombre d'éléments de G est alors noté |G| et est appelé ordre du groupe.

On supposera dans la suite que G est un groupe fini.

Soit . Comme G est fini, le principe de Dirichlet (ou des cages à pigeons) permet de montrer que l'ensemble est non vide. Il admet donc un plus petit élément, que l'on appelle l'ordre de g.

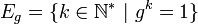
Attention au risque de confusion, ici le terme ordre désigne successivement deux concepts différents, mais il y a quand même un lien, voir ci dessous (groupe cyclique).

L'ordre d d'un élément g possède une propriété arithmétique très utile (qui provient directement de la division euclidienne) :

Soit n un entier non nul tel que gⁿ=1, alors d divise n.

Un sous-ensemble S de G engendre ce groupe si tous les éléments de G s'écrivent comme un produit d'éléments ou d'inverses d'éléments de S. L'ensemble S est appelé une partie génératrice de G.

Comme G est fini, l'inverse d'un élément g est une puissance de g (plus précisément, on a g^-1=g^d-1, où d désigne l'ordre de g). Il suit donc qu'un sous-ensemble S de G est une partie génératrice si et seulement si tout élément de G est un produit d'éléments de S.

Un groupe (fini ou pas) engendré par un singleton {g} est dit cyclique. Par abus de langage, on dit que l'élément g engendre G, et on note alors . Il est facile de vérifier qu'un tel groupe est nécessairement abélien.

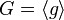
Remarquons que l'ordre d'un groupe cyclique fini est égal à l'ordre d'un de ses générateurs.

Tous les éléments d'un groupe fini G ont un ordre inférieur ou égal à |G|.

Un résultat fondamental dans l'étude des groupes finis est le théorème de Lagrange :

Soient G un groupe fini et H un sous-groupe de G, alors l'ordre de H divise l'ordre de G.

Une conséquence immédiate est que si G est un groupe d'ordre m, alors tout élément g de G vérifie g^m=1 (considérer le sous-groupe engendré par g).

Exemples

Voici quelques exemples classiques de groupes finis :

• le groupe des racines n-ièmes de l'unité : où  ;

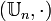
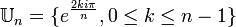
• le groupe des classes résiduelles modulo n :  ;

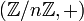
• les groupes symétriques,  : groupes des bijections d'un ensemble fini dans lui-même ;

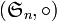
• les groupes diédraux,  : groupes des isométries planes qui conservent un polygone régulier à n côtés ;

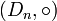
• le groupe de quaternions ;

• le groupe de Klein.

Les deux premiers exemples désignent en fait le même groupe. Pour comprendre ce qu'on entend par même, on va introduire la notion de morphisme de groupe.

Parité de l'ordre et involution

Si un groupe fini possède au moins une involution (élément d'ordre 2) alors, d'après le théorème de Lagrange, ce groupe est d'ordre pair.

Réciproquement, dans un groupe fini d'ordre pair, le nombre d'involution(s) est impair d'après le théorème de Cauchy sur les éléments d'ordre p, donc ce nombre n'est pas nul.

En conclusion l'ordre d'un groupe fini est

• impair s'il n'a pas d'involution,
• pair s'il possède au moins une involution.