Surjection - Définition
La liste des auteurs de cet article est disponible ici.
Exemples
Exemple concret
On considère le cas d'une station de vacances où un groupe de touristes doit être logé dans un hôtel. Chaque façon de répartir ces touristes dans les chambres de l'hôtel peut être représentée par une application de l'ensemble X des touristes vers l'ensemble Y des chambres (à chaque touriste est associée une chambre).
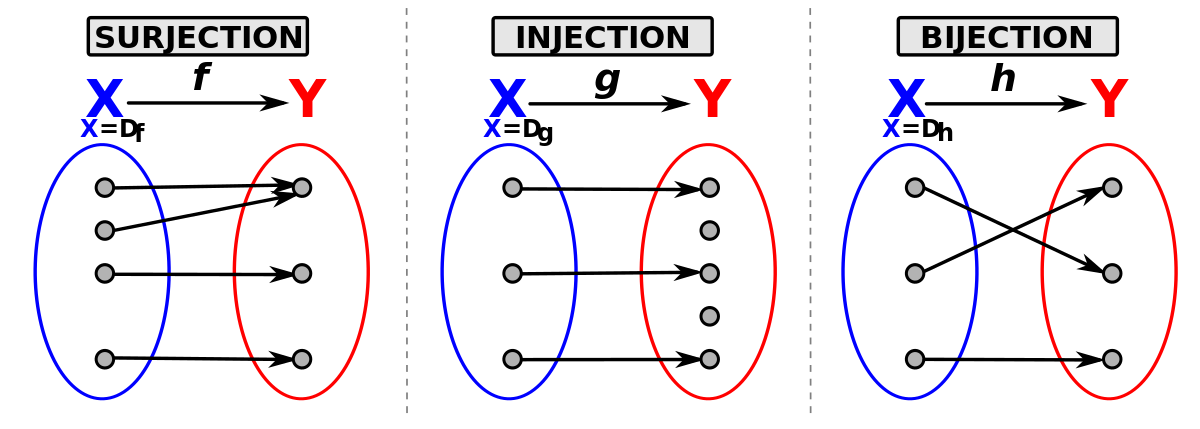
- Les touristes souhaitent que l'application soit injective, c'est-à-dire que chacun d'entre eux ait une chambre individuelle. Cela n'est possible que si le nombre de touristes ne dépasse pas le nombre de chambres.
- L'hôtelier souhaite que l'application soit surjective, c'est-à-dire que chaque chambre soit occupée. Cela n'est possible que s'il y a au moins autant de touristes que de chambres.
- Ces desiderata ne sont compatibles que si le nombre de touristes est égal au nombre de chambres. Dans ce cas, il sera possible de répartir les touristes de telle sorte qu'il y en ait un seul par chambre, et que toutes les chambres soient occupées : l'application sera alors à la fois injective et surjective ; on dira qu'elle est bijective.
Exemples et contre-exemples dans les fonctions réelles
La fonction définie par
n'est pas surjective car certains réels ne possèdent pas d'antécédent. Par exemple, il n'y a pas de réel x tel que f(x) = -4. Mais si on change la définition de f en donnant comme ensemble d'arrivée R+, alors elle le devient car chaque réel positif y possède au moins un antécédent : 0 possède exactement un antécédent, 0, et tous les réels y strictement positifs en possèdent deux, la racine carrée de y et son opposé.
La fonction définie par
est surjective puisque, pour tout réel arbitraire y, il existe des solutions à l'équation y = 2x + 1 d'inconnue x ; une solution est x = (y − 1)/2.
La fonction définie par
n'est pas surjective car les réels strictement plus grands que 1 ou strictement plus petits que -1 n'ont pas d'antécédent.
Mais la fonction définie par
qui possède la même expression que g, mais avec un ensemble d'arrivée qui a été restreint à l'ensemble des réels compris entre -1 et 1, est surjective. En effet, pour tout réel arbitraire y de l'intervalle [-1, 1], il existe des solutions à l'équation y = cos(x) d'inconnue x : ce sont les réels
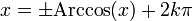
Sur ces quelques exemples, on voit qu'il est toujours possible de transformer une application non surjective en une surjection à condition de restreindre son ensemble d'arrivée.
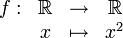
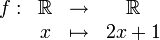
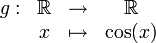
![\begin{matrix}h: & \R & \rightarrow& [-1;1]\\ & x & \mapsto &\cos(x)\\\end{matrix}](https://static.techno-science.net/illustration/Definitions/autres/7/78ee53beb27feca63a29e43f7520a980_38b9173376ff0b33c0c6b8a693129ca4.png)