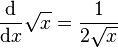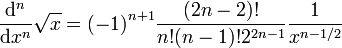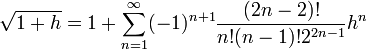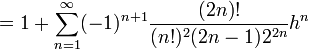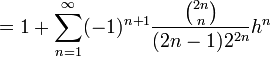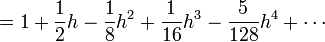Racine carrée - Définition

Introduction

La racine carrée d’un nombre réel positif x est le nombre positif dont le carré vaut x. On le note ou x^½; dans cette expression, x est appelé le radicande.

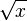
Une tablette d'argile datée du XVIII^e siècle av. J.-C. montre que les Babyloniens connaissaient la racine carrée de deux et un algorithme de calcul.

Tout nombre réel x positif possède une racine carrée qui est elle-même un nombre réel. La racine carrée d'un nombre entier n est soit un entier, soit un nombre irrationnel, c'est-à-dire qu'elle ne peut être exprimée par une fraction. La racine carrée est à l'origine de la découverte de l'irrationnalité, mais contrairement à une idée répandue, rien n'assure que celle de 2 fut le premier nombre irrationnel connu. L'exemple de démonstrations par l'absurde choisi par Aristote, l'un des fondateurs de la logique est fondé sur l'irrationnalité de 2 : «  Ils prouvent que le diamètre du carré est incommensurable au côté en montrant que, si l'on admet qu'il lui est commensurable, un nombre impair serait égal à un pair. »

À la Renaissance, des mathématiciens ont été amenés à définir la racine carrée d'un nombre négatif, ce qui a conduit à l'avènement des nombres complexes. L'extraction d'une racine carrée était la cinquième « opération classique », elle est aussi perçue comme une fonction.

Histoire

Photographie de la tablette YBC 7289 avec des annotations traduisant les nombres écrits dans le système babylonien (crédits : Bill Casselman).

La plus ancienne racine carrée connue apparaît vers 1 700 av. J.-C. sur la tablette YBC 7289. Il s'agit de la représentation d'un carré avec, sur un côté, le nombre 30 et, le long de la diagonale, un valeur approchée de √2.

Fonction réelle

L’application est une bijection dont l’inverse est noté . Cette fonction s’appelle la fonction racine carrée. Géométriquement, on peut affirmer que la racine carrée de l’aire d’un carré du plan euclidien est la longueur de ses côtés.

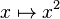
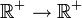
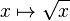
Analyse

La fonction racine carrée vérifie les propriétés élémentaires suivantes valables pour tous nombres réels positifs x et y :

(sous la condition )

.

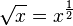
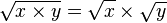
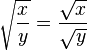
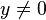
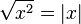
La fonction racine est continue en tout réel positif x (pour y proche de x, est proche de ). Mieux, cette fonction est 1/2-höldérienne. De plus, elle est dérivable en tout réel strictement positif x, mais elle n’est pas dérivable en x=0. En ce point, la pente de la tangente est infinie ; la courbe représentative admet en 0 une demi-tangente verticale.

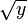
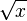
La fonction dérivée de est donnée par :

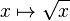
La fonction racine est en réalité de classe sur .

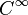
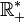
Mieux encore, la fonction racine est développable en séries entières. Le développement en série de Taylor de la fonction racine carrée au point 1 s’obtient immédiatement à partir de la formule du binôme généralisée :

pour tout réel |h| < 1.

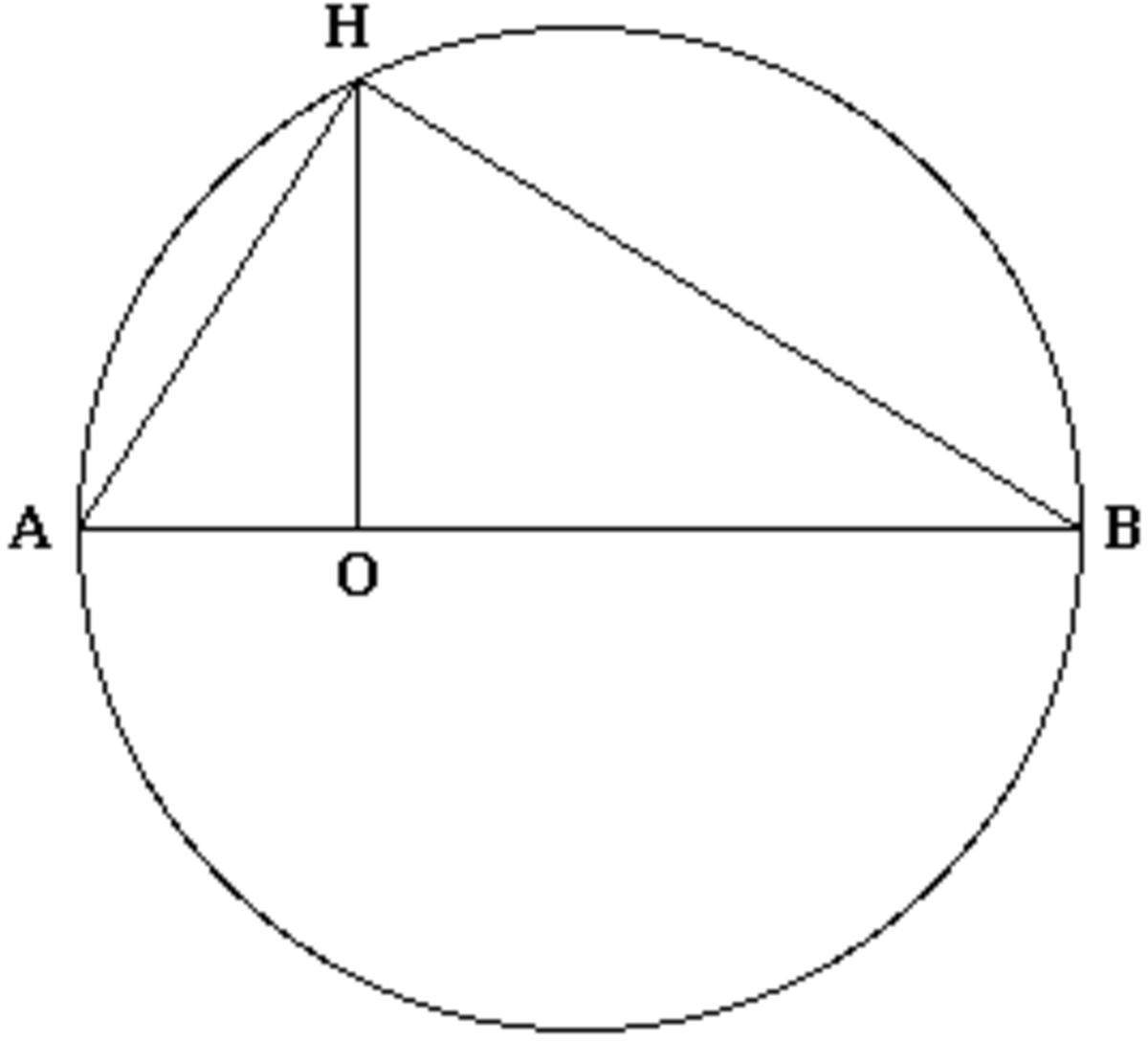
Construction géométrique de la racine carrée

AO = 1, OB = a, OH = x

La construction géométrique suivante se réalise à la règle et au compas et permet, étant donné un segment OB de longueur a, de construire un segment de longueur  :

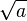
• Construire le segment AB de longueur 1+a et contenant le point O avec AO = 1
• Construire le cercle C de diamètre AB.
• Construire la droite D perpendiculaire à (OB) et passant par O.
• Nommer H le point d’intersection du cercle C et de la droite D.

Le segment OH est de longueur .

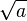
La preuve consiste à appliquer le théorème de Pythagore :

• Au triangle rectangle HOB : OH² + a² = HB²
• Au triangle rectangle ABH : HB² = (a+1)² - AH²
• Au triangle rectangle AOH : AH² = 1² + OH²

D’où OH² + a² = (a+1)² - (1² + OH²), soit, après simplification OH² = a, et donc .

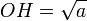
Cette construction a son importance dans l’étude des nombres constructibles.