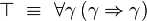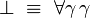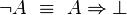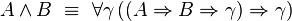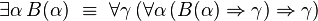Système F - Définition

Correspondance avec la logique du second ordre

À travers la correspondance de Curry-Howard, le système F correspond très exactement à la logique minimale intuitionniste du second ordre, dont les formules sont construites à partir des variables propositionnelles à l'aide de l'implication et de la quantification propositionnelle:

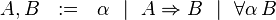
Rappelons que dans ce cadre, les unités (vérité) et (absurdité), les connecteurs (négation), (conjonction) et (disjonction) et la quantification existentielle sont définissables par

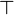
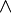
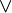
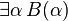
(On notera qu'à travers la correspondance de Curry-Howard, l'absurdité correspond au type vide, la vérité au type singleton, la conjonction au produit cartésien et la disjonction à la somme directe.)

On démontre que dans ce formalisme, une formule est prouvable sans hypothèses si et seulement si le type correspondant dans le système F est habité par un terme clos.

Le théorème de normalisation forte

Les termes typables du système F sont fortement normalisables.

Bibliographie

• Lambda-calcul, types et modèles, Jean-Louis Krivine, chapitre VIII, Masson, 1990, ISBN 2225820910
• Proofs and Types, Jean-Yves Girard, Paul Taylor, Yves Lafont, chapitre 11, Cambridge University Press, 1989, ISBN 0521371813