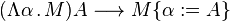Système F - Définition

Introduction

Le système F (également connu sous le nom de lambda-calcul polymorphe ou de lambda-calcul du second ordre) est une extension du lambda-calcul simplement typé introduite indépendamment par le logicien Jean-Yves Girard et par l'informaticien John C. Reynolds. Ce système se distingue du lambda-calcul simplement typé par l'introduction d'un mécanisme de quantification universelle de type qui permet d'exprimer le polymorphisme paramétrique.

Ainsi que l'atteste sa double origine, le système F peut être étudié dans deux contextes très différents:

• Dans le domaine de la programmation fonctionnelle, où il apparaît comme une extension très expressive du noyau du langage ML. Son expressivité est illustrée par le fait que les types de données courants (booléens, entiers, listes, etc.) sont définissables dans le système F à partir des constructions de base.

• Dans le domaine de la logique, et plus particulièrement de la théorie de la démonstration. À travers la correspondance de Curry-Howard, le système F est en effet isomorphe à la logique minimale intuitionniste du second ordre. En outre, ce système capture très exactement la classe des fonctions numériques dont l'existence est prouvable en arithmétique intuitionniste du second ordre (parfois appelée analyse intuitionniste). C'est d'ailleurs cette propriété remarquable du système F qui a historiquement motivé son introduction par Jean-Yves Girard, dans la mesure où cette propriété permet de résoudre le problème de l'élimination des coupures en arithmétique du second ordre, conjecturé par Takeuti.

Comme le lambda-calcul simplement typé, le système F admet deux présentations équivalentes:

• Une présentation à la Church, dans laquelle chaque terme contient toutes les annotations de type nécessaires à la reconstruction de son type (de manière univoque).

• Une présentation à la Curry, due à l'informaticien Daniel Leivant, dans laquelle les termes (qui sont ceux du lambda-calcul pur) sont dépourvus de toute annotation de type, et sont ainsi sujets aux problèmes d'ambiguïté typique.

Présentation à la Church

La syntaxe

Les types du système F (notés A, B, C, etc.) sont formés à partir d'un ensemble de variables de types (notées α, β, γ, etc.) à l'aide des trois règles de construction suivantes:

• (Variable de type) Si α est une variable de type, alors α est un type;
• (Type flèche) Si A et B sont des types, alors est un type;
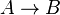
• (Type universel) Si α est une variable de type et B un type, alors est un type.

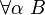
En résumé, les types du système F sont donnés par la grammaire BNF:

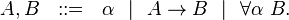
Comme en lambda-calcul ou en calcul des prédicats, la présence d'un symbole mutificateur nécessite de distinguer les notions de variable libre et de variable liée, et d'introduire les mécanismes usuels de renommage permettant de travailler à α-conversion près. Enfin, l'algèbre de types du système F est munie d'une opération de substitution similaire à celle du lambda-calcul, et l'on note B{α: = A} le type obtenu en remplaçant dans le type B toutes les occurrences libres de la variable de type α par le type A.

Les termes (bruts) du système F (notés M, N, etc.) sont formés à partir d'un ensemble de variables de termes (notées x, y, z, etc.) à l'aide des cinq règles de construction suivantes:

• (Variable) Si x est une variable de terme, alors x est un terme;
• (Abstraction) Si x est une variable de terme, A un type et M un terme, alors λx:A.M est un terme;
• (Application) Si M et N sont des termes, alors MN est un terme;
• (Abstraction de type) Si α est une variable de type et M un terme, alors Λα.M est un terme;
• (Application de type) Si M est un terme et A un type, alors MA est un terme.

En résumé, les termes (bruts) du système F sont donnés par la grammaire BNF:

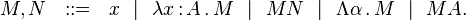
Les termes du système F incorporent deux mécanismes de liaison de variable: un mécanisme de liaison de variables de termes (par la construction ) et un mécanisme de liaison de variables de types (par la construction ), qui sont tous les deux pris en compte au niveau de la relation d'α-conversion. Ce double mécanisme donne naturellement lieu à deux opérations de substitution: une substitution de terme notée M{x: = N}, et une substitution de type notée M{α: = A}.

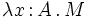
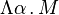
La β-réduction

La présence d'un double mécanisme d'abstraction et d'application (abstraction/application de terme et abstraction/application de type) donne lieu à deux règles de β-réduction, dont l'union engendre par passage au contexte la relation de β-réduction en une étape du système F:

Comme pour le lambda-calcul pur, la β-réduction du système F est confluente (sur les termes bruts) et vérifie la propriété de Church-Rosser:

• (Confluence de la β-réduction) Si et , alors il existe un terme M' tel que et .
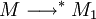
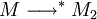
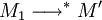
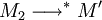
• (Propriété de Church-Rosser) Pour que deux termes M₁ et M₂ soient β-convertibles, il faut et il suffit qu'il existe un terme M' tel que et .

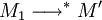
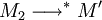
Le système de types

On appelle contexte de typage (notation: Γ, Γ', etc.) toute liste finie de déclarations de la forme x:A (où x est une variable de terme et A un type) dans laquelle une variable de terme est déclarée au plus une fois.

Le système de types du système F est construit autour d'un jugement de typage de la forme (« dans le contexte Γ, le terme M a pour type A »), qui est défini à partir des règles d'inférence suivantes:

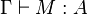
• (Axiome) si

• ( -intro)

• ( -élim)

• ( -intro) si α n'a pas d'occurrence libre dans Γ

• ( -élim) .

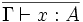
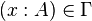
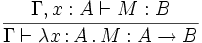
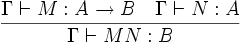
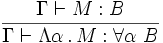
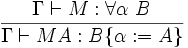
Les deux propriétés principales de ce système de types sont la propriété de préservation du type par β-réduction et la propriété de normalisation forte:

• (Préservation du type par réduction) Si et si , alors .

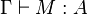
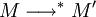
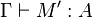
• (Normalisation forte) Si , alors M est fortement normalisable.

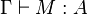
La première de ces deux propriétés est une propriété purement combinatoire qui se démontre par une induction directe sur la dérivation de typage. En revanche, la propriété de normalisation forte du système F est une propriété dont la démonstration repose fondamentalement sur des méthodes non-combinatoires, basées sur la notion de candidat de réductibilité.