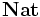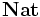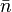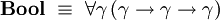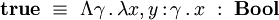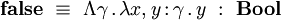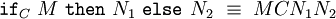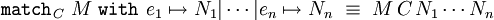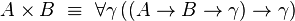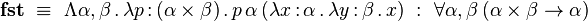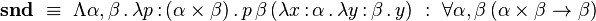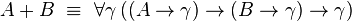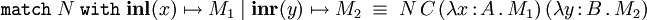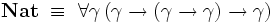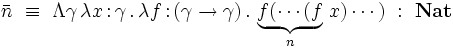Système F - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Présentation à la Church - Présentation à la Curry - Représentation des types de données - Correspondance avec la logique du second ordre - Le théorème de normalisation forte - Bibliographie

Présentation à la Curry

La fonction d'effacement

$| x | = x$
$| λ x : A . M | = λ x . | M |$
$| M N | = | M | | N |$
$| Λα. M | = | M |$
$| M A | = | M |$

Le système de types

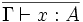
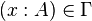
(Axiome) $\frac{}{\Gamma\vdash x:A}$ si $(x:A)\in\Gamma$

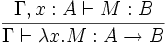
( $\to$ -intro) $\frac{\Gamma,x:A\vdash M:B}{\Gamma\vdash\lambda x.M:A\to B}$

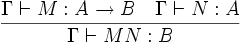
( $\to$ -élim) $\frac{\Gamma\vdash M:A\to B\quad\Gamma\vdash N:A}{\Gamma\vdash MN:B}$

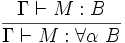
( $\forall$ -intro) $\frac{\Gamma\vdash M:B}{\Gamma\vdash M:\forall\alpha~B}$ si $α$ n'a pas d'occurrence libre dans $Γ$

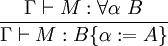
( $\forall$ -élim) $\frac{\Gamma\vdash M:\forall\alpha~B}{\Gamma\vdash M:B\{\alpha:=A\}}$ .

Équivalence entre les deux systèmes

Représentation des types de données

Pour pouvoir utiliser le lambda-calcul simplement typé comme un langage de programmation, il est nécessaire de lui adjoindre des types de base (booléens, entiers, etc.) et des règles de réduction supplémentaires qui étendent le pouvoir expressif du formalisme. Un exemple d'une telle extension est le système T de Gödel, qui est obtenu en ajoutant au lambda-calcul simplement typé des entiers naturels primitifs et un mécanisme de récursion similaire à la récursion primitive (mais plus expressif).

Dans le système F, une telle extension n'est pas nécessaire car l'expressivité du formalisme permet de définir les types de base et les constructeurs de types usuels sans qu'il soit nécessaire de modifier ni le système de types ni les règles de réduction.

Booléens et types finis

Le type des booléens est défini dans le système F par

$\textbf{Bool}~\equiv~\forall\gamma\,(\gamma\to\gamma\to\gamma)$

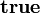
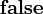
et les constantes $\textbf{true}$ et $\textbf{false}$ par:

$\textbf{true}~\equiv~\Lambda\gamma\,.\,\lambda x,y\,{:}\,\gamma\,.\,x~:~\textbf{Bool}$
$\textbf{false}~\equiv~\Lambda\gamma\,.\,\lambda x,y\,{:}\,\gamma\,.\,y~:~\textbf{Bool}$

On peut démontrer que les deux termes ci-dessus sont les deux seuls termes clos en forme normale de type . Ainsi, le type de données capture effectivement la notion de booléen.

La construction 'if ... then ... else ...' est définie par

$\texttt{if}_C~M~\texttt{then}~N_1~\texttt{else}~N_2~\equiv~MCN_1N_2$

où $C$ désigne le type d'élimination de la construction 'if ...', c'est-à-dire le type commun aux deux branches de la conditionnelle. Cette définition est correcte du point de vue du typage comme du point de vue calculatoire dans la mesure où:

Dans tout contexte où le terme $M$ a le type et où les termes $N 1$ et $N 2$ ont le type $C$ , la construction est bien typée et a pour type le type $C$ .

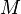
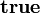
Si le terme $M\,\!$ se réduit sur $\textbf{true}$ , alors la construction se réduit sur $N_1\,\!$ .
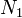
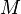
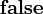
Si le terme $M\,\!$ se réduit sur $\textbf{false}$ , alors la construction se réduit sur $N_2\,\!$ .

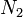
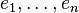
Plus généralement, on peut définir un type fini $E n$ à $n$ valeurs $e_1,\ldots,e_n$ en posant

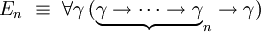
$E_n~\equiv~\forall\gamma\,(\underbrace{\gamma\to\cdots\to\gamma}_n\to\gamma)$
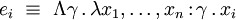
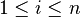
$e_i~\equiv~\Lambda\gamma\,.\,\lambda x_1,\ldots,x_n\,{:}\,\gamma\,.\,x_i$ (pour tout $1\le i\le n$ )

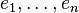
Là encore, on peut démontrer que les termes $e_1,\ldots,e_n$ sont les seuls termes clos en forme normale de type $E n$ . L'opération de filtrage correspondant est définie par:

$\texttt{match}_C~M~\texttt{with}~e_1\mapsto N_1|\cdots|e_n\mapsto N_n~\equiv~M\,C\,N_1\cdots N_n$

(où $C$ désigne le type des branches de filtrage).

En particulier:

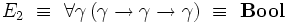
$E_2~\equiv~\forall\gamma\,(\gamma\to\gamma\to\gamma)~\equiv~\textbf{Bool}$ (type des booléens)
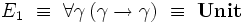
$E_1~\equiv~\forall\gamma\,(\gamma\to\gamma)~\equiv~\textbf{Unit}$ (type singleton)
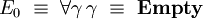
$E_0~\equiv~\forall\gamma\,\gamma~\equiv~\textbf{Empty}$ (type vide)

Le type $E 0$ n'est habité par aucun terme clos en forme normale, et, d'après le théorème de normalisation forte, qu'il n'est habité par aucun terme clos.

Produit cartésien et somme directe

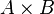
Soit $A$ et $B$ deux types. Le produit cartésien $A\times B$ est défini dans le système F par

$A\times B~\equiv~\forall\gamma\,((A\to B\to\gamma)\to\gamma)$

et la construction de couple par

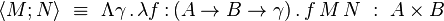
$\langle M;N\rangle~\equiv~\Lambda\gamma\,.\,\lambda f\,{:}\,(A\to B\to\gamma)\,.\,f\,M\,N~:~A\times B$ (si $M:A\,\!$ et $N:B\,\!$ )

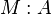
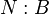
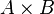
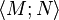
Comme pour les types énumérés, on peut démontrer que les seuls termes clos en forme normale de type $A\times B$ sont de la forme $\langle M;N\rangle$ , où $M$ et $N$ sont des termes clos en forme normale de type $A$ et $B$ , respectivement. Les fonctions de projection correspondantes sont données par

$\textbf{fst}~\equiv~\Lambda\alpha,\beta\,.\,\lambda p\,{:}\,(\alpha\times\beta)\,.\,p\,\alpha\,(\lambda x\,{:}\,\alpha\,.\,\lambda y\,{:}\,\beta\,.\,x)~:~\forall\alpha,\beta\,(\alpha\times\beta\to\alpha)$
$\textbf{snd}~\equiv~\Lambda\alpha,\beta\,.\,\lambda p\,{:}\,(\alpha\times\beta)\,.\,p\,\beta\,(\lambda x\,{:}\,\alpha\,.\,\lambda y\,{:}\,\beta\,.\,y)~:~\forall\alpha,\beta\,(\alpha\times\beta\to\beta)$

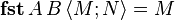
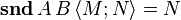
Ces fonctions vérifient naturellement les égalités $\textbf{fst}\,A\,B\,\langle M;N\rangle=M$ et $\textbf{snd}\,A\,B\,\langle M;N\rangle=N$ .

La somme directe $A + B$ est définie par

$A+B~\equiv~\forall\gamma\,((A\to\gamma)\to(B\to\gamma)\to\gamma)$

Les habitants des types $A$ et $B$ sont plongés dans le type $A + B$ à l'aide des constructions

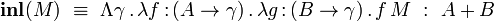
$\textbf{inl}(M)~\equiv~\Lambda\gamma\,.\,\lambda f\,{:}\,(A\to\gamma)\,.\,\lambda g\,{:}\,(B\to\gamma)\,.\,f\,M~:~A+B$ (si $M:A\,\!$ )
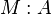
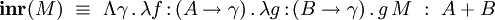
$\textbf{inr}(M)~\equiv~\Lambda\gamma\,.\,\lambda f\,{:}\,(A\to\gamma)\,.\,\lambda g\,{:}\,(B\to\gamma)\,.\,g\,M~:~A+B$ (si $M:B\,\!$ )

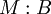
tandis que le filtrage des éléments de type $A + B$ est assuré par la construction

$\texttt{match}~N~\texttt{with}~\textbf{inl}(x)\mapsto M_1~|~\textbf{inr}(y)\mapsto M_2~\equiv~N\,C\,(\lambda x\,{:}\,A\,.\,M_1)\,(\lambda y\,{:}\,B\,.\,M_2)$

qui satisfait les égalités définitionnelles attendues.

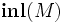
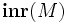
Contrairement au produit cartésien, l'encodage de la somme directe dans le système F ne capture pas toujours la notion d'union disjointe, dans la mesure où il est possible, dans certains cas, de construire des termes clos en forme normale de type $A + B$ qui ne sont ni de la forme $\textbf{inl}(M)$ (avec $M : A$ ) ni de la forme $\textbf{inr}(M)$ (avec $M : B$ ).

Les entiers de Church

Le type des entiers de Church est défini dans le système F par

$\mathbf{Nat}~\equiv~\forall\gamma\,(\gamma\to(\gamma\to\gamma)\to\gamma)$

Chaque entier naturel $n$ est représenté par le terme

$\bar{n}~\equiv~\Lambda\gamma\,\lambda x\,{:}\,\gamma\,.\,\lambda f\,{:}\,(\gamma\to\gamma)\,.\,\underbrace{f(\cdots(f}_n\,x)\cdots)~:~\mathbf{Nat}$

Comme pour les booléens, le type $\mathbf{Nat}$ capture la notion d'entier naturel puisque tout terme clos de type $\mathbf{Nat}$ en forme normale est de la forme $\bar{n}$ pour un certain entier naturel $n$ .

Présentation à la Church

Correspondance avec la logique du second ordre

Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋

Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️

Des singularités temporelles dans l'Univers ? 🕰️

Des fossiles de dinosaures mieux datés 🦖

Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭

Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆

Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜

Le rôle méconnu de la décharge dans l'usure des batteries 🔋

La fonte des glaces déplace les pôles: quelles conséquences ? 🌍

L'appareil photo de votre smartphone peut détecter l'antimatière 📱

Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐

Un mosasaure géant découvert dans le Mississippi 🦕

Problème, les galaxies meurent plus tôt que prévu 🌀

Ce lien entre cannabis et troubles psychotiques 🧠

Une révolution dans le refroidissement des puces électroniques ? 🔥

Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀

Lucy survole un astéroïde en forme de cacahuète 🚀

Découverte du fossile d'un dinosaure géant méconnu 🦕

Mars avait-elle un champ magnétique unilatéral ? 🔍

Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇

Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁

L'électroluminescence du graphène, une découverte inattendue ! 💡

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Page générée en 0.132 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise