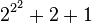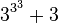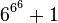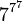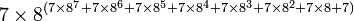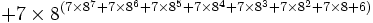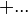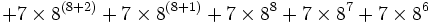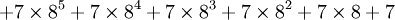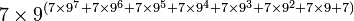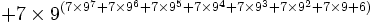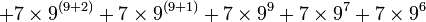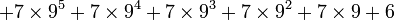Théorème de Goodstein - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définition d'une suite de Goodstein - Preuve - Exemples de suites de Goodstein - Bibliographie

Exemples de suites de Goodstein

Les premières suites de Goodstein se terminent rapidement. Par exemple G(3):

Base	Notation héréditaire	Valeur	Notes
2	2¹ + 1	3	Le 1 représente 2⁰.
3	3¹ + 1 − 1 = 3	3	On change 2 en 3, puis on soustrait 1
4	4¹ − 1 = 3	3	On change 3 en 4 puis on soustrait 1
5	3 − 1 = 2	2	Puisque la base utilisée est supérieure aux chiffres de la décomposition, les changements de base ultérieurs sont sans effet.
6	2 − 1 = 1	1
7	1 − 1 = 0	0

Les suites de Goodstein croissent en général pendant un grand nombre d'étapes. Par exemple, la suite G(4) commence comme suit :

Notation héréditaire	Valeur
2²	4
2·3² + 2·3 + 2	26
2·4² + 2·4 + 1	41
2·5² + 2·5	60
2·6² + 6 + 5	83
2·7² + 7 + 4	109
...
2·11² + 11	253
2·12² + 11	299
...
2·23²	1058
24²+23·24+23	1151
...

La suite G(4) continue à croître.

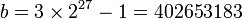
Lorsqu'on atteint la base $b = 3 \times 2^{27} -1 = 402653183$ , le terme de la suite vaut b² = 162129585780031489.

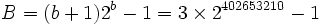
Lorsqu'on atteint la base $B = (b+1)2^b -1 = 3 \times 2^{402653210} - 1$ , le terme de la suite vaut B.

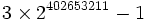
La suite se met enfin à décroître, et atteint la valeur nulle pour la base $3 \times 2^{402653211} - 1$ qui, curieusement, est un nombre de Woodall, comme toutes les autres bases finales pour des valeurs initiales supérieures à 4. La base à laquelle la suite G(4) se termine possède plus de 120 millions de chiffres, ce qui signifie que le nombre de termes de la suite G(4) est de l'ordre de $10120000000$ .

Cependant, l'exemple de G(4) ne donne pas encore une idée suffisante de la vitesse à laquelle la suite de Goodstein peut croître. G(19) croît beaucoup plus rapidement et commence comme suit :

Notation héréditaire	Valeur
$2^{2^2}+2+1$	19
$3^{3^3}+3$	7625597484990
$4^{4^4}+3$	environ 1.3 × 10¹⁵⁴
$5^{5^5}+2$	environ 1.8 × 10²¹⁸⁴
$6^{6^6}+1$	environ 2.6 × 10³⁶³⁰⁵
$7^{7^7}$	environ 3.8 × 10⁶⁹⁵⁹⁷⁴
$7 \times 8^{(7 \times 8^7 + 7 \times 8^6 + 7 \times 8^5 + 7 \times 8^4 + 7 \times 8^3 + 7 \times 8^2 + 7 \times 8 + 7)}$ $+ 7 \times 8^{(7 \times 8^7 + 7 \times 8^6 + 7 \times 8^5 + 7 \times 8^4 + 7 \times 8^3 + 7 \times 8^2 + 7 \times 8 + 6)}$ $+ ... \,\;$ $+ 7 \times 8^{(8+2)} + 7 \times 8^{(8+1)} + 7 \times 8^8 + 7 \times 8^7 + 7 \times 8^6$ $+ 7 \times 8^5 + 7 \times 8^4 + 7 \times 8^3 + 7 \times 8^2 + 7 \times 8 + 7$	environ 6 × 10^15151335
$7 \times 9^{(7 \times 9^7 + 7 \times 9^6 + 7 \times 9^5 + 7 \times 9^4 + 7 \times 9^3 + 7 \times 9^2 + 7 \times 9 + 7)}$ $+ 7 \times 9^{(7 \times 9^7 + 7 \times 9^6 + 7 \times 9^5 + 7 \times 9^4 + 7 \times 9^3 + 7 \times 9^2 + 7 \times 9 + 6)}$ $+ ... \,\;$ $+ 7 \times 9^{(9+2)} + 7 \times 9^{(9+1)} + 7 \times 9^9 + 7 \times 9^7 + 7 \times 9^6$ $+ 7 \times 9^5 + 7 \times 9^4 + 7 \times 9^3 + 7 \times 9^2 + 7 \times 9 + 6$	environ 4.3 × 10^369693099
...

En dépit de sa rapide croissance, le théorème de Goodstein établit que chaque suite de Goodstein se termine par 0, quelle que soit la valeur initiale de m. À titre d'exemple, le nombre de termes de la suite G(5) se calcule comme suit. Posons :

g (n) = n 2 n

k fois

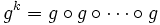
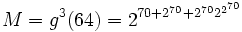
N = g M (M), P = g N (N), Q = g P (P)

Le nombre de termes de la suite G(5) est alors Q-1.

Bibliographie

R. Goodstein, « On the restricted ordinal theorem », dans Journal of Symbolic Logic, 9 (1944), 33-41

L. Kirby et J. Paris, « Accessible independence results for Peano arithmetic », dans Bull. London. Math. Soc., 14 (1982), 285-93

Patrick Dehornoy, « L'infini est-il nécessaire ? », dans Pour la Science, 278 (2000), 102-106

Preuve

- Introduction - Définition d'une suite de Goodstein - Preuve - Exemples de suites de Goodstein - Bibliographie

🌍 Les dernières mesures révèlent un niveau de CO₂ jamais vu depuis 4 millions d'années

🛡️ Le paradoxe des gangs de rue

💰 Quelle quantité d'or existe-t-il vraiment sur Terre ?

🦟 Pourquoi les moustiques sont plus nombreux et piquent davantage en été ?

⚫ Ces trous noirs interagissent avec la lumière fossile du Big Bang

🦕 Et si les dinosaures détenaient le secret pour vaincre le cancer ?

😎 Comment font les lunettes de soleil pour filtrer les UV ?

🚶‍♂️‍➡️ La marche des babouins éclaire l'évolution de la bipédie humaine

🔭 James Webb capture cette image directe d'une étrange planète à 60 années-lumière

🦋 Pourquoi et comment les chenilles deviennent-elles des papillons ?

🔭 Voici la plus grande carte de l'Univers. Ses révélations sont surprenantes !

😴 Penser que l'on est éveillé alors que l'on dort, normal ?

🌊 Ce cratère raconte l'histoire de l'eau sur Mars

🐝 Comment les fleurs attirent-elles les insectes pollinisateurs ?

💥 La collision entre notre Voie lactée et la galaxie d'Andromède remise en question

🎶 Pourquoi les oiseaux chantent-ils autant et si fort au printemps ?

💡 Générer de la lumière à partir du vide, c'est possible

Découverte d'un deuxième système d'apprentissage dans le cerveau

☀️ Comment se produit un coup de chaleur et comment s'en protéger ?

⚽ Comment fonctionne la physique d'un tir puissant au foot ?

🧠 Un algorithme révèle comment notre cerveau se motive

🔭 Une si grande planète orbite une si petite étoile, comment est-ce possible ?

🐋 Les baleines développent de nouvelles méthodes pour communiquer avec nous

🥚 Le noyau de Mars sent l'œuf pourri

🧠 On sait enfin pourquoi le sémaglutide fait maigrir

🌱 La vie pourrait renaître sur Europe après la mort de la Terre

🌿 Confirmation scientifique: ce remède ancestral fait naturellement maigrir, et pas qu'un peu !

💥 Des astronomes identifient les plus puissantes explosions depuis le Big Bang

🦕 Ce crâne de stégosaure, le plus complet jamais découvert, réécrit l'histoire

🛏️ Les punaises de lit, ces compagnons indésirables depuis la préhistoire

🕸️ Connaissez-vous la toile cosmique, l'architecte de l'Univers ?

🌋 L'éruption de l'Etna vue depuis l'espace

🐋 Il y a 20 000 ans, l'Homme fabriquait des outils avec des os de baleines

🟠 Quel est le rôle de ce labyrinthe sur Mars ?

🎯 Cette stratégie innovante contre le cancer du sein offre une survie de 100%

💥 Le pulsar à trou noir: un objet qui intrigue les astrophysiciens

🐒 Première: ces singes kidnappent les bébés d'une autre espèce

🌍 Découverte d'une super-Terre à l'habitabilité intermittente

🧠 Ces cellules pourraient jouer un rôle bien plus important que les neurones dans la mémoire

🛰️ Une carte photographique de la Terre toutes les 35 minutes

Pourquoi l'oxygène est-il si indispensable à autant d'êtres vivants ?

🐱 Pourquoi certains chats miaulent et ronronnent plus que d'autres ?

Découverte: un antidouleur sans effets secondaires

🤔 Ces expériences remettent en question un concept fondamental de la thermodynamique

Le cannabis réduit de moitié la fonction des vaisseaux sanguins

Les différences hommes-femmes ne sont pas que génétiques

🦴 Des paresseux géants de plusieurs tonnes parcouraient autrefois l'Amérique

James Webb découvre une nouvelle population de trous noirs supermassifs

Le sol de l'Afrique du Sud s'est soulevé ces dernières années, pourquoi ?

👀 Ces lentilles de contact permettent de voir l'invisible

Page générée en 0.113 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise