Théorème de Herbrand - Définition

Le théorème de Herbrand

Considérons alors une formule F universelle (ou un ensemble de formules), par exemple du type , où P est un prédicat, et soit un ensemble de variables a₁,a₂,...,a_n,.... Considérons les trois propriétés :

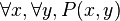
1. F est consistante, i.e on ne peut déduire une contradiction de l'hypothèse F. Ou encore n'est pas prouvable dans un système de déduction du calcul des prédicats, telle la déduction naturelle par exemple, ce qu'on note : .
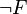
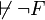
2. F est satisfiable, i.e. il existe un modèle dans lequel F est vraie, ce qu'on note : .
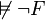
3. Pour tout entier n, il existe un modèle dans lequel la proposition suivante que nous noterons Q(a₁,...,a_n) est vraie :

ce qu'on note : pour tout n,

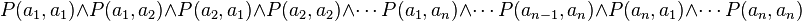
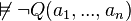
Le théorème de complétude de Gödel énonce l'équivalence entre 1) et 2). Par ailleurs, 2) entraîne 3), le modèle dans lequel 2) est vérifié permettant d'en déduire des modèles vérifiant 3). Le théorème de Herbrand énonce que, réciproquement, 3) entraîne 2), lorsque les a_i décrivent un domaine particulier, le domaine de Herbrand. On constate que, dans la formulation de 3), les quantificateurs universels ont disparu et que les formules à prouver deviennent alors de simples propositions du calcul propositionnel.

De manière duale, en posant et , on obtient les équivalences entre les trois propriétés :

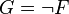
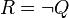
1. G est prouvable, i.e il existe une démonstration de G dans un système de déduction du calcul propositionnel. ce qu'on note : .
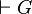
2. G est valide, i.e. G est vraie dans tout modèle, ce qu'on note : .
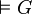
3. Il existe un entier n pour lequel R(a₁,...,a_n) est valide :

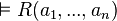
G est alors un théorème.

Si F n'est pas satisfiable (ce qui se produit si et seulement si est un théorème), alors en vérifiant Q(a₁,...,a_n) pour n = 1, puis n = 2, etc., on finira par tomber sur un entier n tel que Q(a₁,...,a_n) est fausse, et réciproquement.

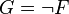
Par contre, si F est satisfiable (et donc si G n'est pas un théorème), alors pour tout n, Q(a₁,...,a_n) sera vraie, et le processus de calcul ne se terminera pas, sauf dans le cas particulier où les variables a_i sont en nombre fini.

Cela illustre le fait que l'ensemble des formules non satisfiables ou l'ensemble des théorèmes sont des ensembles récursivement énumérables, mais que le calcul des prédicats n'est pas décidable.