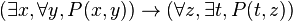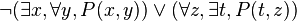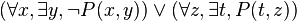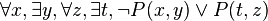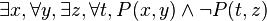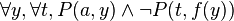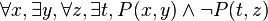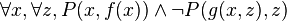Théorème de Herbrand - Définition

Introduction

En logique, le théorème de Herbrand établit un lien entre calcul des prédicats et calcul des propositions. Alors qu'il est possible de déterminer de manière certaine si une proposition du calcul des propositions est démontrable ou pas, la question équivalente pour une formule du calcul des prédicats est plus délicate. Le théorème de Herbrand répond partiellement à cette question, bien qu'on sache depuis les travaux de Gödel, Tarski, Church, Turing et autres, qu'il n'existe pas d'algorithme permettant de décider si une formule générale du calcul des prédicats est prouvable ou non.

Formules prénexes

Une formule du calcul des prédicats est prénexe si tous les quantificateurs qu'elle contient se trouvent au début de la formule. Toute formule est équivalente à une formule prénexe. Par exemple, la formule est équivalente successivement à , , et enfin (où désignent respectivement l'implication, la négation, la disjonction, la conjonction. P et Q sont des prédicats unaires).

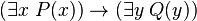
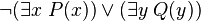
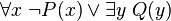
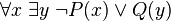
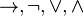
Une formule prénexe est universelle si elle ne possède que des quantificateurs universels (i.e. de symbole : ). Il est possible d'associer à une formule quelconque une formule universelle en lui appliquant une transformation de Skolem, consistant à introduire de nouveaux symboles de fonctions pour chaque quantificateur existentiel (i.e. de symbole : ). Par exemple, la forme skolémisée de est . Intuitivement, si pour chaque x, il existe y tel qu'une propriété R(x,y) soit vérifiée, alors on peut introduire une fonction f(x) = y telle que, pour tout x, R(x,f(x)) est vérifiée. On montre que la formule initiale admet un modèle si et seulement si sa forme skolémisée en admet un. Autrement dit, la formule initiale est satisfiable si et seulement si sa forme skolémisée l'est. De même, la formule initiale est insatisfiable si et seulement si sa forme skolémisée l'est, et donc la négation de la formule initiale est prouvable si et seulement si la négation de sa forme skolémisée l'est.

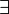
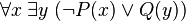
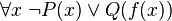
Exemples

Le domaine de Herbrand du modèle est défini au moins par un élément constant (afin d'être non vide) et est constitué de tous les termes que l'on peut former à partir des constantes et des fonctions utilisées dans les formules considérées. On définit un modèle de Herbrand en attribuant la valeur vraie à certains prédicats définis sur ces termes.

Exemple 1 : On considère la formule , où a est une constante. Le domaine de Herbrand est constitué du singleton {a}. On forme alors la formule qui est fausse, donc F n'est pas satisfiable.

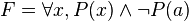
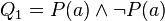
Exemple 2 : On considère la formule . Le domaine de Herbrand est {a,b}. On forme alors qui est vraie dans un modèle où l'on donne la valeur vraie à Q(a), puis on forme qui est vraie dans un modèle où l'on donne la valeur vraie à {Q(a),P(b)}. Ayant épuisé le domaine de Herbrand, le calcul se termine et F est satisfiable dans le modèle précédemment défini.

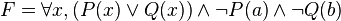
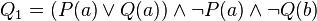
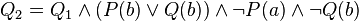
Exemple 3 : On considère la formule . Le domaine de Herbrand est constitué de {a,f(a),f²(a),...,fⁿ(a),...}. On forme alors qui possède un modèle en attribuant la valeur vraie à P(a) mais fausse à P(f(a)). Puis, en prenant les deux premiers éléments du domaine a et f(a), on forme qui ne peut posséder de modèle à cause de la conjonction fausse . Donc F ne possède pas de modèle.

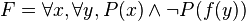
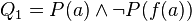
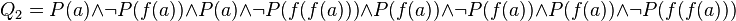
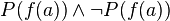
Exemple 4 : On considère la formule dont on veut montrer qu'il s'agit d'un théorème. Après avoir renommé les variables x et y dans la deuxième partie de G afin d'éviter d'avoir des variables liées de même nom, on obtient une forme prénexe équivalente à G :

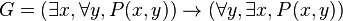
La formule prénexe F équivalente à est :

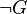
dont la forme skolémisée est :

La formation des formules Q₁ en prenant pour (y,t) le couple (a,a) puis Q₂ en prenant (y,t) = (f(a),a) conduit à qui est fausse dans tout modèle. F n'est donc pas satisfiable et G est un théorème.

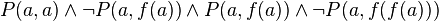
Exemple 5 : On considère la formule . Par un procédé comparable à l'exemple précédent, on obtient pour forme prénexe équivalente à G : . La formule prénexe F équivalente à est :

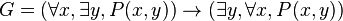
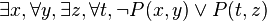
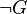
dont la forme skolémisée est :

Elle est satisfiable en donnant la valeur vrai à tout P(u,f(u)) et faux à tout P(g(u,v),v), où u et v décrivent le domaine de Herbrand {a,f(a),g(a,a),f(f(a)),f(g(a,a)),g(a,f(a)),...}, et en donnant une valeur arbitraire aux autres prédicats. Cependant, le calcul successif des formules correspondantes Q₁, Q₂, ... ne se termine pas. F est satisfiable et donc G n'est pas un théorème, mais la démarche précédente ne permet pas de le montrer par un calcul en un nombre fini d'étapes.