Théorème de la base incomplète - Définition

Applications

Soit E un K-espace vectoriel et F un sous-espace vectoriel de E Alors F possède un supplémentaire dans E, i.e. il existe un sous-espace vectoriel G de E tel que . En effet, c'est clair si F={0} ou F=E; sinon, on considère une base B de F qu'on complète en une base B' de E: l'espace engendré par les vecteurs de B' qui ne sont pas dans F convient.

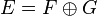
Le corps des réels R est défini comme une extension du corps des rationnels Q, et en ce sens, il peut être vu comme un Q-espace vectoriel (la multiplication par un scalaire rationnel est simplement la multiplication usuelle de réels). Le théorème de la base incomplète implique l'existence d'une base de R comme Q-espace vectoriel. Les vecteurs de cette base forment un ensemble A , et si r et s appartiennent à A alors r-s est irrationnel. L'ensemble A n'est ni borélien ni Lebesgue-mesurable. Sa construction repose sur le théorème de la base incomplète et donc sur l'axiome du choix.