Théorème du rang - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Cas des matrices
Le théorème du rang peut s'écrire pour les matrices. Si A est une matrice (m,n) sur un corps

- rgA + dim(KerU) = n
où U est l'application linéaire de
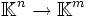
Certains définissent le noyau d'une matrice de la manière suivante :
-
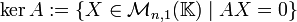
qui est un sous-espace vectoriel de
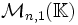
Le théorème du rang s'écrit alors
- rgA + dim(KerA) = n.

















































