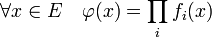Sous-espace vectoriel - Définition

Introduction

En algèbre linéaire, étant donné un espace vectoriel E sur un corps K, un sous-espace vectoriel de E est une partie non vide F de E stable par combinaisons linéaires. Autrement dit, cette partie doit vérifier :

• La somme vectorielle de deux vecteurs de F appartient à F ;
• La multiplication d'un vecteur de F par un scalaire appartient à F.

Ces conditions imposent à ce que le vecteur nul appartienne à F. Muni des lois induites, F est un K-espace vectoriel. l'espace nul {0} et l'espace total E sont respectivement les plus petit et plus grand sous-espaces vectoriels de E. En général, une réunion finie de sous-espaces vectoriels n'est pas stable par combinaisons linéaires. Cependant, étant donnée une famille de sous-espaces vectoriels de E, son intersection est un sous-espace vectoriel de E. La somme de la famille est le plus petit sous-espace contenant tous les F_i.

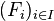
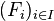
Définition équivalente

Le sous-ensemble F est un -sous-espace vectoriel de E si et seulement si :

• 
•  ;
•  ;
• .

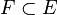
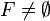
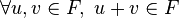
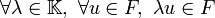
Ceci équivaut à :

• 
• ;
• .

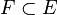
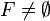
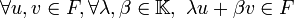
En d'autres termes, F est un sous-espace vectoriel de E si et seulement s'il n'est pas vide et est stable par combinaisons linéaires.

Nota : dans tout espace vectoriel E non réduit à , il y a au moins deux sous-espaces vectoriels. Ce sont et E lui-même : on les appelle les deux sous-espaces vectoriels triviaux.

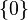
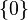
Remarque 1 : un sous-espace vectoriel F de E contient nécessairement le vecteur nul de E (en effet, comme F est non vide, il existe au moins un élément de F ; alors, pour tout dans , λu₀ appartient à F ; le choix donne ).

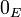
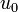
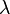
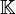
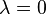
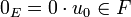
C'est pourquoi, lorsqu'il s'agit de montrer qu'un sous-ensemble F de E est un sous-espace vectoriel de E, on vérifie souvent que F ne soit pas vide en s'assurant qu'il contient le vecteur nul (s'il ne le contient pas, il y a immédiatement contradiction).

Remarque 2 : lorsque E n'est pas réduit à , on définit dans l'ensemble une relation d'équivalence R qui consiste à dire que deux éléments V et W sont liés par R s'il existe un élément k non nul du corps commutatif K tel que W = k V. Alors P, l'ensemble quotient de G par R, a une structure très riche d'espace projectif.

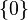
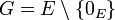
Union de sous-espaces vectoriels

Dans le cas général, la structure de sous-espace vectoriel n'est pas stable par l'union. Il existe deux propositions traitant ce cas.

• E est ici de dimension finie, et son corps associé est de cardinal infini. Si (F_i) est une famille finie de sous-espaces vectoriels de E et tous différents de E, alors l'union de la famille (F_i) est différente de E.

• Si (F_i) est une famille de sous-espaces vectoriels de E telle que l'union de deux éléments de cette famille soit toujours incluse dans un troisième élément de la famille, alors l'union de la famille (F_i) est un sous-espace vectoriel de E.